定义在R上的函数f(x)满足f(2x)=2f2(x)-1,现给定下列几个命题:
(1)f(x)≥-1;
(2)f(x)不可能是奇函数;
(3)f(x)不可能是常数函数;
(4)若f(x)=a(a>1),则不存在常数M,使得f(x)≤M恒成立;
在上述命题中错误命题的个数为( )个.
A.4
B.3
C.2
D.1
【答案】
分析:本题是一个多选题,对抽象表达式f(2x)=2f2(x)-1表达的函数性质进行推断,应该注意函数f(x)=cosx符合此表达式,易判断①②③的真假,至于选项④,显然不是函数f(x)=cosx的性质,应为真命题
解答:解:(1)∵f(x)=f(2×
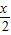
)=2f
2(
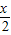
)-1≥-1,故(1)正确
(2)∵f(0)=2f
2(0)-1,解得f(0)=1或-

,即f(0)≠0,f(x)不可能为奇函数,故(2)正确
(3)若f(x)=1,或f(x)=-

,则函数f(x)满足f(2x)=2f
2(x)-1,故(3)错误
(4)若f(x
)=a(a>1),则此函数没有上界,即不存在常数M,使得f(x)≤M成立,故④正确
故选D
点评:本题考查了抽象函数表达式的意义,解题时要能透过现象看到本质,熟练的运用特殊函数,特殊值等方法准确做出判断

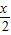 )=2f2(
)=2f2(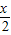 )-1≥-1,故(1)正确
)-1≥-1,故(1)正确 ,即f(0)≠0,f(x)不可能为奇函数,故(2)正确
,即f(0)≠0,f(x)不可能为奇函数,故(2)正确 ,则函数f(x)满足f(2x)=2f2(x)-1,故(3)错误
,则函数f(x)满足f(2x)=2f2(x)-1,故(3)错误

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案