
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() ,
,![]() 的中点.
的中点.
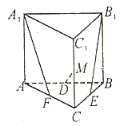
(I)证明:直线![]() 与
与![]() 共面;
共面;
(Ⅱ)证明:平面![]() 平面
平面![]() ;并试写出
;并试写出![]() 到平面
到平面![]() 的距离(不必写出计算过程).
的距离(不必写出计算过程).
【答案】(I)证明见解析;(Ⅱ)证明见解析.
【解析】
(I)由中位线的性质可得![]() ,再由棱柱的性质可得
,再由棱柱的性质可得![]() ,根据平行线的传递性可得
,根据平行线的传递性可得![]() ,从而得到四点共面,即可得证;
,从而得到四点共面,即可得证;
(Ⅱ)首先可得![]() ,再由线面垂直的性质得到
,再由线面垂直的性质得到![]() ,从而得到
,从而得到![]() 平面
平面![]() ,再根据
,再根据![]() ,即可得到
,即可得到![]() 平面
平面![]() ,从而得证;设
,从而得证;设![]() ,则
,则![]() 平面
平面![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,可得
,可得![]() 即为
即为![]() 到平面
到平面![]() 的距离,再在三角形中利用勾股定理及相似三角形的性质计算可得.
的距离,再在三角形中利用勾股定理及相似三角形的性质计算可得.
解:(I)证明:![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,
由棱柱性质易得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,即直线
四点共面,即直线![]() 与
与![]() 共面.
共面.
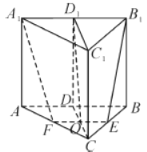
(Ⅱ)同(I)易证四边形![]() 为平行四边形,又
为平行四边形,又![]() ,
,![]() 为
为![]() 中点,则
中点,则![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() 得证.
得证.
![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
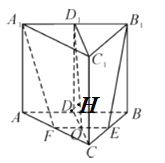
(解答)如图,设![]() ,则
,则![]() 平面
平面![]() 平面
平面![]() ,过
,过![]() 作
作![]() 于
于![]() ,可得
,可得![]() 即为
即为![]() 到平面
到平面![]() 的距离.在
的距离.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,又
,又![]() ,则在
,则在![]() 中,
中,![]()
故![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1).设a=2,b=![]() .
.
(1)求方程f(x)=2的根;
(2)若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福彩是利国利民游戏,其刮刮乐之《蓝色奇迹》:如图(1)示例,刮开票面看到最左侧一列四个两位数字为“我的号码”,最上行四个两位数为“中奖号码”,这八个两位数是00至99这一百个数字随机产生的,若两个数字相同即中得其相交线上的奖金,奖金可以累加.小明买的一张《蓝色奇迹》刮刮乐如图(2),除了一个“我的号码”外,他已经刮开票面上其它所有数字,依据目前的信息,小明从这张刮刮乐得到的奖金额高于600元的概率为(无所得税)( )


图(1) 图(2)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了减轻家庭困难的高中学生的经济负担,让更多的孩子接受良好的教育,国家施行高中生国家助学金政策,普通高中国家助学金平均资助标准为每生每年1500元,具体标准由各地结合实际在1000元至3000元范围内确定,可以分为两或三档.各学校积极响应政府号召,通过各种形式宣传国家助学金政策.为了解某高中学校对国家助学金政策的宣传情况,拟采用随机抽样的方法抽取部分学生进行采访调查.
(1)若该高中学校有2000名在校学生,编号分别为0001,0002,0003,…,2000,请用系统抽样的方法,设计一个从这2000名学生中抽取50名学生的方案.(写出必要的步骤)
(2)该校根据助学金政策将助学金分为3档,1档每年3000元,2档每年2000元,3档每年1000元,某班级共评定出3个1档,2个2档,1个3档,若从该班获得助学金的学生中选出2名写感想,求这2名同学不在同一档的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
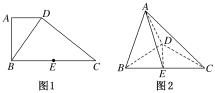
若AD=1,二面角CABD的平面角的正切值为![]() ,求二面角BADE的余弦值.
,求二面角BADE的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
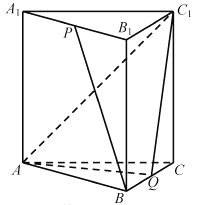
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点.
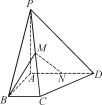
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com