
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的单凋区间;
的单凋区间;
(2)若函数![]() 是函数
是函数![]() 的图像的切线,求
的图像的切线,求![]() 的最小值;
的最小值;
(3)求证:![]() .
.
【答案】(1) ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为区间为
,单调减区间为区间为![]() ;(2)
;(2) ![]() ;(3) 见解析.
;(3) 见解析.
【解析】试题分析: (1)先求函数导数,再在定义域内求导函数零点,列表分析导函数符号变化规律,确定单调区间,(2)先设切点![]() ,根据导数几何意义将
,根据导数几何意义将![]() 表示成
表示成![]() 的函数:
的函数:![]() ,再利用导数求函数最小值,(3)利用结论
,再利用导数求函数最小值,(3)利用结论![]() ,进行放缩
,进行放缩![]()
![]() ,转化证明
,转化证明![]() ,这可以构造差函数
,这可以构造差函数![]() ,利用导数可得其最大值为
,利用导数可得其最大值为![]() .
.
试题解析: (1)![]() 时,
时,![]()
![]() ,
,
![]() ,
,![]() ,
,
解![]() 得
得![]() ,解
,解![]() 得
得![]() ,
,
∴![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为区间为
,单调减区间为区间为![]() .
.
(2)设切点坐标为设切点坐标为![]() ,
,
![]() ,
,
切线斜率![]() ,又
,又![]() ,
,
∴![]() ,∴
,∴![]()
令![]() ,
,
![]()
![]()
![]() ,
,
解![]() 得
得![]() ,解
,解![]() 得
得![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增.
上递增.
∴![]() ,∴
,∴![]() 的最小值为
的最小值为![]() .
.
(3)法一:令![]() ,
,
由(1)知![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]()
![]()
∴![]() ,(两个等号不会同时成立)
,(两个等号不会同时成立)
∴![]() .
.
法二:令![]() ,
,![]()
显然![]() 在
在![]() 上递增,
上递增,![]() ,
,![]()
∴![]() 在
在![]() 上有唯一实根
上有唯一实根![]() ,且
,且![]() ,
,![]()
![]() ,
,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
∴![]()
![]()
![]()
![]()
![]()
∴![]() ,
,


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某校为了解学生一周的课外阅读情况,随机抽取了100名学生对其进行调查.下面是根据调查结果绘制的一周学生阅读时间(单位:分钟)的频率分布直方图,且将一周课外阅读时间不低于200分钟的学生称为“阅读爱好”,低于200分钟的学生称为“非阅读爱好”.
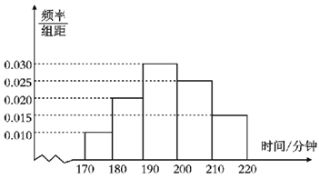
(1)根据已知条件完成下面![]() 列联表,并据此判断是否有97.5%的把握认为“阅读爱好”与性别有关?
列联表,并据此判断是否有97.5%的把握认为“阅读爱好”与性别有关?
非阅读爱好 | 阅读爱好 | 合计 | |
男女 | 50 | ||
合计 | 14 | ||
男女 |
(2)将频率视为概率,从该校学生中用随机抽样的方法抽取4人,记被抽取的四人中“阅读爱好”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B﹣PADE的体积是![]() ;
;

(1)画出面PBE与面ABC的交线,说明理由;
(2)求面PBE与面ABC所成的锐二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com