
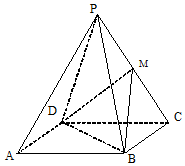
 已知四棱锥P-ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题:
已知四棱锥P-ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题:分析 (1)连结AC、BD交于点O,连结OP,以O为原点,$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OP}$分别为x,y,z轴的正方向,建立空间直角坐标系O-xyz,利用向量法能证明PA∥平面BMD.
(2)求出平面ABCD的法向量和平面MBD的法向量,利用向量法能求出二面角M-BD-C的平面角.
解答 证明:(1)连结AC、BD交于点O,连结OP.…(1分)
∵四边形ABCD是正方形,∴AC⊥BD∵PA=PC,∴OP⊥AC,
同理OP⊥BD,…(2分)
以O为原点,$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OP}$分别为x,y,z轴的正方向,建立空间直角坐标系O-xyz,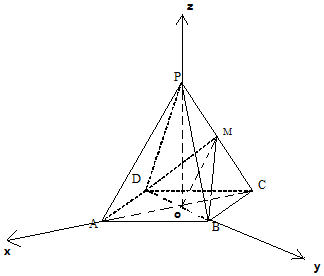
$P(0,0,\sqrt{2}),A(\sqrt{2},0,0),B(0,\sqrt{2},0),M(-\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2})$,…(3分)
$\overrightarrow{PA}=(\sqrt{2},0,-\sqrt{2}),\overrightarrow{OB}=(0,\sqrt{2},0),\overrightarrow{OM}=(-\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2})$,…(4分)
平面BMD的法向量为$\overrightarrow n=(1,0,1)$,
∵$\overrightarrow{PA}•\overrightarrow n=0$,$\overrightarrow{PA}⊥\overrightarrow n$,又PA?平面BMD,…(5分)
∴PA∥平面BMD.…(6分)
解:(2)平面ABCD的法向量为$\overrightarrow a=(0,0,1)$…(7分)
平面MBD的法向量为$\overrightarrow b=(x,y,1)$,
则$\left\{\begin{array}{l}\sqrt{2}y=0\\-\frac{{\sqrt{2}}}{2}x+\frac{{\sqrt{2}}}{2}=0\end{array}\right.$,即$\left\{\begin{array}{l}y=0\\ x=1\end{array}\right.$,…(8分)
∴$\overrightarrow b=(1,0,1)$…(9分)
二面角M-BD-C的平面角为α,
则$cosα=\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,α=45°,…(11分)
∴二面角M-BD-C的平面角45°.…(12分)
点评 本题考查线面平行的证明,考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
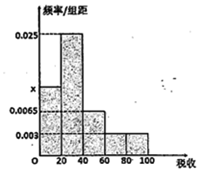 我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]
我市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 科研费用支出(xi) | 利润(yi) |
| 2011 2012 2013 2014 2015 2016 | 5 11 4 5 3 2 | 31 40 30 34 25 20 |
| 合计 | 30 | 180 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $1-\frac{{\sqrt{3}}}{2}$ | D. | $1-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
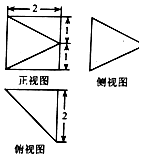
| A. | $\frac{8}{3}$ | B. | 4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com