
°æƒø°ø¥”ƒ≥—ß–£∏þ»˝ƒÍº∂π≤![]() √˚ƒ–…˙÷–Àʪ˙≥È»°
√˚ƒ–…˙÷–Àʪ˙≥È»°![]() √˚≤‚¡ø…Ì∏þ£¨≤‚¡ø∑¢œ÷±ª≤‚—ß…˙…Ì∏þ»´≤øΩÈ”⁄
√˚≤‚¡ø…Ì∏þ£¨≤‚¡ø∑¢œ÷±ª≤‚—ß…˙…Ì∏þ»´≤øΩÈ”⁄![]() ∫Õ
∫Õ![]() ÷ƺ‰£¨Ω´≤‚¡øΩ·π˚∞¥»Áœ¬∑Ω Ω∑÷≥…∞À◊È£¨µ⁄“ª◊È
÷ƺ‰£¨Ω´≤‚¡øΩ·π˚∞¥»Áœ¬∑Ω Ω∑÷≥…∞À◊È£¨µ⁄“ª◊È![]() £ªµ⁄∂˛◊È
£ªµ⁄∂˛◊È![]() £¨
£¨![]() £¨µ⁄∞À◊È
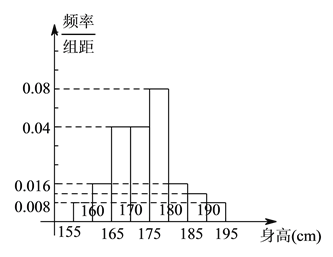
£¨µ⁄∞À◊È![]() £¨»ÁÕº «∞¥…œ ˆ∑÷◊È∑Ω∑®µ√µΩµƒ∆µ¬ ∑÷≤º÷±∑ΩÕºµƒ“ª≤ø∑÷£¨»Ùµ⁄“ª◊Ȕε⁄∞À◊È»À ˝œýÕ¨£¨µ⁄¡˘◊È°¢µ⁄∆þ◊È°¢µ⁄∞À◊È»À ˝“¿¥Œππ≥…µ»≤Ó ˝¡–£Æ
£¨»ÁÕº «∞¥…œ ˆ∑÷◊È∑Ω∑®µ√µΩµƒ∆µ¬ ∑÷≤º÷±∑ΩÕºµƒ“ª≤ø∑÷£¨»Ùµ⁄“ª◊Ȕε⁄∞À◊È»À ˝œýÕ¨£¨µ⁄¡˘◊È°¢µ⁄∆þ◊È°¢µ⁄∞À◊È»À ˝“¿¥Œππ≥…µ»≤Ó ˝¡–£Æ

£®![]() £©π¿º∆’‚À˘—ß–£∏þ»˝ƒÍº∂»´Ãƒ–…˙…Ì∏þ
£©π¿º∆’‚À˘—ß–£∏þ»˝ƒÍº∂»´Ãƒ–…˙…Ì∏þ![]() “‘…œ£®∫¨
“‘…œ£®∫¨![]() £©µƒ»À ˝£Æ
£©µƒ»À ˝£Æ
£®![]() £©«Ûµ⁄¡˘◊È°¢µ⁄∆þ◊ȵƒ∆µ¬ ≤¢≤π≥‰ÕÍ’˚∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ£®«¶± ◊˜Õº≤¢”√÷––‘± √Ë∫⁄£©£Æ
£©«Ûµ⁄¡˘◊È°¢µ⁄∆þ◊ȵƒ∆µ¬ ≤¢≤π≥‰ÕÍ’˚∆µ¬ ∑÷≤º÷±∑ΩÕº£Æ£®«¶± ◊˜Õº≤¢”√÷––‘± √Ë∫⁄£©£Æ
£®![]() £©»Ù¥”…Ì∏þ Ù”⁄µ⁄¡˘◊È∫Õµ⁄∞À◊ȵƒÀ˘”–ƒ–…˙÷–Àʪ˙≥È»°¡Ω√˚ƒ–…˙£¨º«À˚√«µƒ…Ì∏þ∑÷±Œ™
£©»Ù¥”…Ì∏þ Ù”⁄µ⁄¡˘◊È∫Õµ⁄∞À◊ȵƒÀ˘”–ƒ–…˙÷–Àʪ˙≥È»°¡Ω√˚ƒ–…˙£¨º«À˚√«µƒ…Ì∏þ∑÷±Œ™![]() °¢
°¢![]() £¨«Û¬˙◊„
£¨«Û¬˙◊„![]() µƒ ¬º˛∏≈¬ £Æ
µƒ ¬º˛∏≈¬ £Æ
°æ¥∞∏°ø£®1£©9»À£ª£®2£©º˚Ω‚Œˆ£ª£®3£©![]()
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©”…∆µ¬ ∑÷≤º÷±∑ΩÕºø…µ√«∞ŒÂ◊È∆µ¬ £¨Ω¯∂¯ø…µ√∫Û»˝◊È∆µ¬ ∫Õ»À ˝£¨”÷ø…µ√∫Û»˝◊ȵƒ»À ˝£¨ø…µ√∆Ωæ˘…Ì∏þ£ª
£®2£©“◊µ√∫Û»˝◊ȵƒ![]() £¨ø…µ√∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£¨ø…µ√∆µ¬ ∑÷≤º÷±∑ΩÕº£ª
£®3£©”…£®![]() £©÷™…Ì∏þ‘⁄
£©÷™…Ì∏þ‘⁄![]() ƒ⁄µƒ»À ˝Œ™
ƒ⁄µƒ»À ˝Œ™![]() »À£¨
»À£¨
…Ë![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() °£…Ì∏þŒ™
°£…Ì∏þŒ™![]() µƒ»À ˝Œ™
µƒ»À ˝Œ™![]() »À£¨
»À£¨
…ËŒ™![]() £¨
£¨![]() £Æ£¨¡–æŸø…µ√◊еƒª˘±æ ¬º˛π≤15÷÷«Èøˆ£¨ ¬º˛°∞
£Æ£¨¡–æŸø…µ√◊еƒª˘±æ ¬º˛π≤15÷÷«Èøˆ£¨ ¬º˛°∞![]() °±À˘∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝”–6+1=7£¨”…∏≈¬ π´ Ωø…µ√£Æ
°±À˘∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝”–6+1=7£¨”…∏≈¬ π´ Ωø…µ√£Æ
‘Ã‚Ω‚Œˆ£∫£®![]() £©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷™£¨
£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷™£¨
«∞ŒÂ◊È∆µ¬ Œ™![]() £¨
£¨
∫Û»˝◊È∆µ¬ Œ™![]() £¨»À ˝Œ™
£¨»À ˝Œ™![]() »À£¨
»À£¨
’‚À˘—ß–£∏þ»˝ƒ–…˙…Ì∏þ‘⁄![]() “‘…œ£®∫¨
“‘…œ£®∫¨![]() £©µƒ»À ˝Œ™
£©µƒ»À ˝Œ™![]() »À£Æ
»À£Æ
£®![]() £©”…∆µ¬ ∑÷≤º÷±∑ΩÕºµ√µ⁄∞À◊È∆µ¬ Œ™
£©”…∆µ¬ ∑÷≤º÷±∑ΩÕºµ√µ⁄∞À◊È∆µ¬ Œ™![]() £¨»À ˝Œ™
£¨»À ˝Œ™![]() »À£¨
»À£¨
…˵⁄¡˘◊È»À ˝Œ™![]() £¨‘Úµ⁄∆þ◊È»À ˝Œ™
£¨‘Úµ⁄∆þ◊È»À ˝Œ™![]() £¨”÷
£¨”÷![]() £¨À˘“‘
£¨À˘“‘![]() £¨
£¨
º¥µ⁄¡˘◊È»À ˝Œ™![]() »À£¨µ⁄∆þ◊È»À ˝Œ™
»À£¨µ⁄∆þ◊È»À ˝Œ™![]() »À£¨∆µ¬ ∑÷±Œ™
»À£¨∆µ¬ ∑÷±Œ™![]() £¨
£¨![]() £¨
£¨
∆µ¬ ≥˝“‘◊Èæý∑÷±µ»”⁄![]() £¨
£¨![]() £¨º˚Õº£Æ
£¨º˚Õº£Æ
£®![]() £©”…£®
£©”…£®![]() £©÷™…Ì∏þ‘⁄
£©÷™…Ì∏þ‘⁄![]() ƒ⁄µƒ»À ˝Œ™
ƒ⁄µƒ»À ˝Œ™![]() »À£¨
»À£¨
…Ë![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() °£…Ì∏þŒ™
°£…Ì∏þŒ™![]() µƒ»À ˝Œ™
µƒ»À ˝Œ™![]() »À£¨
»À£¨
…ËŒ™![]() £¨
£¨![]() £Æ
£Æ
»Ù![]() £¨
£¨![]() ±£¨”–
±£¨”–![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() π≤¡˘÷÷«Èøˆ£Æ
π≤¡˘÷÷«Èøˆ£Æ
»Ù![]() £¨
£¨![]() ±£¨”–
±£¨”–![]() π≤“ª÷÷«Èøˆ£Æ
π≤“ª÷÷«Èøˆ£Æ
»Ù![]() £¨
£¨![]() ∑÷±‘⁄
∑÷±‘⁄![]() £¨
£¨![]() ƒ⁄ ±£¨
ƒ⁄ ±£¨
”–![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() π≤
π≤![]() ÷÷«Èøˆ£Æ
÷÷«Èøˆ£Æ
À˘“‘ª˘±æ ¬º˛µƒ◊Ð ˝Œ™![]() ÷÷£Æ
÷÷£Æ
¬º˛![]() À˘∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝”–
À˘∞¸∫¨µƒª˘±æ ¬º˛∏ˆ ˝”–![]() ÷÷£¨π
÷÷£¨π ![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–Àµ∑®£∫¢Ÿ≤–≤Óø…”√¿¥≈–∂œƒ£–Õƒ‚∫œµƒ–ßπ˚;
¢⁄…Ë”–“ª∏ˆªÿπÈ∑Ω≥Ã![]() £¨±‰¡øx‘ˆº”“ª∏ˆµ•Œª ±£¨y∆Ωæ˘‘ˆº”5∏ˆµ•Œª£ª
£¨±‰¡øx‘ˆº”“ª∏ˆµ•Œª ±£¨y∆Ωæ˘‘ˆº”5∏ˆµ•Œª£ª
¢€œþ–‘ªÿπÈ∑Ω≥Ã![]() ±ÿπ˝
±ÿπ˝![]() £ª
£ª
¢Ð‘⁄“ª∏ˆ2°¡2¡–¡™±Ì÷–£¨”…º∆À„µ√![]() =13.079£¨‘Ú”–99%µƒ∞—Œ’»∑»œ’‚¡Ω∏ˆ±‰¡øº‰”–πÿœµ£®∆‰÷–
=13.079£¨‘Ú”–99%µƒ∞—Œ’»∑»œ’‚¡Ω∏ˆ±‰¡øº‰”–πÿœµ£®∆‰÷–![]() £©£ª
£©£ª
∆‰÷–¥ÌŒÛµƒ∏ˆ ˝ «£® £©
A. 0 B. 1 C. 2 D. 3.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™¡ÀΩ‚∏þ“ª µ—È∞ýµƒ ˝—ß≥…º®,≤…”√≥È—˘µ˜≤ȵƒ∑Ω Ω,ªÒ»°¡À![]() Œª—ß…˙‘⁄µ⁄“ª—ß∆⁄ƒ©µƒ ˝—ß≥…º® ˝æð,—˘±æÕ≥º∆Ω·π˚»Áœ¬±Ì£∫
Œª—ß…˙‘⁄µ⁄“ª—ß∆⁄ƒ©µƒ ˝—ß≥…º® ˝æð,—˘±æÕ≥º∆Ω·π˚»Áœ¬±Ì£∫
∑÷◊È | ∆µ ˝ | ∆µ¬ |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
∫œº∆ |
|
|
(1)«Û![]() µƒ÷µ∫Õ µ—È∞ý ˝—ß∆Ωæ˘∑÷µƒπ¿º∆÷µ£ª
µƒ÷µ∫Õ µ—È∞ý ˝—ß∆Ωæ˘∑÷µƒπ¿º∆÷µ£ª
(2)»Áπ˚”√∑÷≤„≥È—˘µƒ∑Ω∑®¥” ˝—ß≥…º®–°”⁄![]() ∑÷µƒ—ß…˙÷–≥È»°
∑÷µƒ—ß…˙÷–≥È»°![]() √˚—ß…˙,‘Ÿ¥”’‚
√˚—ß…˙,‘Ÿ¥”’‚![]() √˚—ß…˙÷–—°
√˚—ß…˙÷–—°![]() »À,«Û÷¡…Ÿ”–“ª∏ˆ—ß…˙µƒ ˝—ß≥…º® «‘⁄
»À,«Û÷¡…Ÿ”–“ª∏ˆ—ß…˙µƒ ˝—ß≥…º® «‘⁄![]() µƒ∏≈¬ .
µƒ∏≈¬ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() .
.
(1)«Ûf(2)£¨f(x)£ª
(2)÷§√˜£∫∫Ø ˝f(x)‘⁄[1£¨17]…œŒ™‘ˆ∫Ø ˝£ª
(3) ‘«Û∫Ø ˝f(x)‘⁄[1£¨17]…œµƒ◊Ó¥Û÷µ∫Õ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=![]() £®x
£®x![]() R£©£¨g£®x£©=2a-1
R£©£¨g£®x£©=2a-1
£®1£©«Û∫Ø ˝f£®x£©µƒµ•µ˜«¯º‰”κ´÷µ£Æ
£®2£©»Ùf£®x£©°ðg£®x£©∂‘![]() ∫„≥…¡¢£¨«Û µ ˝aµƒ»°÷µ∑∂Œß.
∫„≥…¡¢£¨«Û µ ˝aµƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…˿Ζƒ¬ Œ™ ![]() µƒÕ÷‘≤E£∫
µƒÕ÷‘≤E£∫ ![]() +
+ ![]() =1£®a£æb£æ0£©µƒ◊Û°¢”“Ωπµ„Œ™F1 £¨ F2 £¨ µ„P «E…œ“ªµ„£¨PF1°ÕPF2 £¨ °˜PF1F2ƒ⁄«–‘≤µƒ∞Îæ∂Œ™
=1£®a£æb£æ0£©µƒ◊Û°¢”“Ωπµ„Œ™F1 £¨ F2 £¨ µ„P «E…œ“ªµ„£¨PF1°ÕPF2 £¨ °˜PF1F2ƒ⁄«–‘≤µƒ∞Îæ∂Œ™ ![]() ©Å1£Æ
©Å1£Æ
£®1£©«ÛEµƒ∑Ω≥ãª
£®2£©æÿ–ŒABCDµƒ¡Ω∂•µ„C°¢D‘⁄÷±œþy=x+2£¨A°¢B‘⁄Õ÷‘≤E…œ£¨»Ùæÿ–ŒABCDµƒ÷Ð≥§Œ™ ![]() £¨«Û÷±œþABµƒ∑Ω≥ãÆ
£¨«Û÷±œþABµƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø”√ø’º‰œÚ¡øΩ‚æˆœ¬¡–Œ £∫»ÁÕº£¨‘⁄–±»˝¿‚÷˘![]() ÷–£¨
÷–£¨ ![]() «
«![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨ ![]() °Õ∆Ω√Ê
°Õ∆Ω√Ê![]() £¨
£¨ ![]() £¨
£¨ ![]() £Æ
£Æ

£®1£©«Û÷§£∫ ![]() £ª
£ª
£®2£©«Û∂˛√ÊΩ«![]() µƒ”ýœ“÷µ£Æ
µƒ”ýœ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤C£∫ ![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™ ![]() £¨”“Ωπµ„Œ™F£¨µ„B£®0£¨1£©‘⁄Õ÷‘≤C…œ£Æ
£¨”“Ωπµ„Œ™F£¨µ„B£®0£¨1£©‘⁄Õ÷‘≤C…œ£Æ
£®¢Ò£©«ÛÕ÷‘≤Cµƒ∑Ω≥ãª
£®¢Ú£©π˝µ„ ![]() µƒ÷±œþΩªÕ÷‘≤C”⁄M£¨N¡Ωµ„£¨Ωª÷±œþx=2”⁄µ„P£¨…Ë
µƒ÷±œþΩªÕ÷‘≤C”⁄M£¨N¡Ωµ„£¨Ωª÷±œþx=2”⁄µ„P£¨…Ë ![]() £¨
£¨ ![]() £¨«Û÷§£∫¶À+¶ÃŒ™∂®÷µ£Æ
£¨«Û÷§£∫¶À+¶ÃŒ™∂®÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨»˝¿‚◊∂A£≠BCD÷–£¨AB°Õ∆Ω√ÊBCD£¨CD°ÕBD .

£®1£©«Û÷§£∫CD°Õ∆Ω√ÊABD£ª
£®2£©»ÙAB£ΩBD£ΩCD£Ω1£¨MŒ™AD÷–µ„£¨«Û»˝¿‚◊∂A£≠MBCµƒÃª˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com