
分析 (1)根据题意可将汽车与A地的距离skm表示为时间t(h)的函数;
(2)求出从A地到B地所用时间,代入函数y=$\frac{1}{128000}$x3-$\frac{3}{80}$x+8(0<x≤120)得答案.
解答 解:(1)根据题意,汽车与A地的距离skm表示为时间t(h)(从A地出发时开始)的函数为:
s=$\left\{\begin{array}{l}{40t,0≤t≤2.5}\\{100,2.5≤t≤3.5}\\{100-50(t-3.5),3.5≤t≤5.5}\end{array}\right.$;
(2)汽车以40km/h的速度从A地到100km远处的B地,共用时2.5小时,
则从A地到B地,该汽车要耗油为y=$\frac{1}{128000}×2.{5}^{3}-\frac{3}{8}×2.5+8$=7.06262207(升).
故从A地到B地,该汽车要耗油7.06262207升.
点评 本题考查函数模型的选择及应用,考查了简单的数学建模思想方法,是中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,0) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
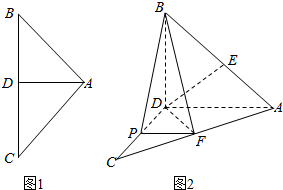 如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:
如图1,AD是等腰直角三角形ABC斜边上的高AB=4,沿AD把△ABC的两部分折成直二面角(如图2),P,E,F分别为CD,CA,BA的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com