
【题目】以下四个命题中正确的个数是( ) (1.)若x∈R,则x2+ ![]() ≥x;
≥x;
(2.)若x≠kπ,k∈Z,则sinx+ ![]() ≥2;
≥2;
(3.)设x,y>0,则 ![]() 的最小值为8;
的最小值为8;
(4.)设x>1,则x+ ![]() 的最小值为3.
的最小值为3.
A.1
B.2
C.3
D.4
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典.其中对勾股定理的论术比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )
寸,估算该木材镶嵌在墙中的体积约为( )
(注:1丈=10尺=100寸, ![]() ,
, ![]() )
)

A. 633立方寸 B. 620立方寸 C. 610立方寸 D. 600立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(2)=4,定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)确定y=g(x)的解析式;
(2)求m,n的值;
(3)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
A.mα,nα,m∥β,n∥βα∥β
B.α∥β,mα,nβ,m∥n
C.m⊥α,m⊥nn∥α
D.m∥n,n⊥αm⊥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC.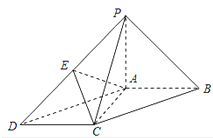
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点.
(Ⅰ)求证:AB⊥平面PAC;
(Ⅱ)求证:AQ∥平面PCD.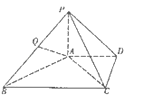
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD. 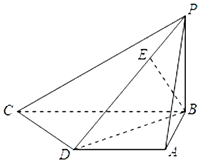
(1)求异面直线PA与CD所成的角的大小;
(2)求证:BE⊥平面PCD;
(3)求二面角A﹣PD﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com