
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 1-2$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
分析 求出可行域的面积,利用点到直线的距离公式转化求解即可.
解答 解:x、y满足不等式组$\left\{\begin{array}{l}{x+y≤1}\\{x-y≥-1}\\{y≥0}\end{array}\right.$的可行域如图:阴影部分三角形,可得三角形的面积为:$\frac{1}{2}×2×1$=1,
直线x-y-a=0平分不等式组所表示的平面区域的面积,面积为:$\frac{1}{2}$,
此时(1,0)到直线x-y-a=0的距离为:1.
可得$\frac{|1-a|}{\sqrt{2}}$=1,
解得a=$1-\sqrt{2}$ .
.
故选:D.
点评 本题考查线性规划的简单应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
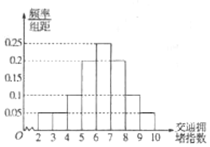 交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2]畅通;T∈[2,4]基本畅通;T∈[4,6]轻度拥堵;T∈[6,8]中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交能指挥中心选取了市区20个交能路段,依据其交能拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6],[6,8],[8,10]的路段中共抽取6个中段,则中度拥堵的路段应抽取3个.
交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2]畅通;T∈[2,4]基本畅通;T∈[4,6]轻度拥堵;T∈[6,8]中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交能指挥中心选取了市区20个交能路段,依据其交能拥堵指数数据绘制的直方图如图所示,用分层抽样的方法从交通指数在[4,6],[6,8],[8,10]的路段中共抽取6个中段,则中度拥堵的路段应抽取3个.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 6 | m | -4 | -6 | -6 | -4 | n | 6 |
| A. | (-3,-1)和(-1,1) | B. | (-3,-1)和(2,4) | C. | (-1,1)和(1,2) | D. | (-∞,-3)和(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{i}{2}$ | B. | -$\frac{i}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {6} | B. | {0,3,5} | C. | {0,3,6} | D. | {0,1,3,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com