
【题目】已知数列{an}前n项和为Sn .
(1)若Sn=2n﹣1,求数列{an}的通项公式;
(2)若a1= ![]() ,Sn=anan+1 , an≠0,求数列{an}的通项公式;
,Sn=anan+1 , an≠0,求数列{an}的通项公式;
(3)设无穷数列{an}是各项都为正数的等差数列,是否存在无穷等比数列{bn},使得an+1=anbn恒成立?若存在,求出所有满足条件的数列{bn}的通项公式;若不存在,说明理由.
【答案】
(1)解:n=1时,a1=S1=2﹣1=1,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣1﹣(2n﹣1﹣1)=2n﹣1,
上式对n=1也成立.
综上可得数列{an}的通项公式为an=2n﹣1;
(2)解:a1= ![]() ,Sn=anan+1,an≠0,
,Sn=anan+1,an≠0,
可得a1=a1a2,a1≠0,可得a2=1,
当n≥2时,an=Sn﹣Sn﹣1=anan+1﹣an﹣1an,
即有an+1﹣an﹣1=1,
即有数列{an}中奇数项和偶数项分别构成公差为1的等差数列,
可得a2n﹣1= ![]() +n﹣1=
+n﹣1= ![]() ,a2n=1+n﹣1=n=
,a2n=1+n﹣1=n= ![]() ,
,
故数列{an}的通项公式为an= ![]() ;
;
(3)解:设an=c+dn,假设存在无穷等比数列{bn},使得an+1=anbn恒成立.
设数列{bn}的公比为q,则bn+1=qbn,
即有 ![]() =q
=q ![]() ,
,
即an+2an=qan+12,
则(dn+2d+c)(dn+c)=q(dn+d+c)2对一切n为自然数成立.
即(d2﹣qd2)n2+2(1﹣q)d(c+d)n+c(2d+c)﹣q(d+c)2=0对n∈N*成立.
取n=1,2,3可得(d2﹣qd2)+2(1﹣q)d(c+d)+c(2d+c)﹣q(d+c)2=0①
4(d2﹣qd2)+4(1﹣q)d(c+d)+c(2d+c)﹣q(d+c)2=0②
9(d2﹣qd2)+6(1﹣q)d(c+d)+c(2d+c)﹣q(d+c)2=0③
由恒成立思想可得d2﹣qd2=0,(1﹣q)d(c+d)=0,c(2d+c)﹣q(d+c)2=0,
当d=0时,an=c>0,所以bn=1(n∈N*),检验满足要求;
当d≠0,q=1,所以c(2d+c)﹣q(d+c)2=0,则d=0,矛盾.
综上可得,当等差数列{an}的公差d=0,存在无穷等比数列{bn},
使得an+1=anbn恒成立,且bn=1;
当等差数列{an}的公差d≠0,不存在无穷等比数列{bn},
使得an+1=anbn恒成立.
【解析】(1)由数列的递推式:n=1时,a1=S1,当n≥2时,an=Sn﹣Sn﹣1,计算即可得到所求通项公式;(2)求出a1=a1a2,a1≠0,可得a2=1,当n≥2时,an=Sn﹣Sn﹣1=anan+1﹣an﹣1an,即有an+1﹣an﹣1=1,即有数列{an}中奇数项和偶数项分别构成公差为1的等差数列,运用等差数列的通项公式即可得到所求通项;(3)设an=c+dn,假设存在无穷等比数列{bn},使得an+1=anbn恒成立.设数列{bn}的公比为q,则bn+1=qbn,
即有 ![]() =q
=q ![]() ,则(dn+2d+c)(dn+c)=q(dn+d+c)2对一切n为自然数成立.展开等式,取n=1,2,3,再由恒成立思想,可得d,q的值,解方程即可判断存在性.
,则(dn+2d+c)(dn+c)=q(dn+d+c)2对一切n为自然数成立.展开等式,取n=1,2,3,再由恒成立思想,可得d,q的值,解方程即可判断存在性.


科目:高中数学 来源: 题型:
【题目】已知常数m≠0,n≥2且n∈N,二项式(1+mx)n的展开式中,只有第6项的二项式系数最大,第三项系数是第二项系数的9倍.
(1)求m、n的值;
(2)若记(1+mx)n=a0+a1(x+8)+a2(x+8)2+…+an(x+8)n , 求a0﹣a1+a2﹣a3+…+(﹣1)nan除以6的余数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆P过A(﹣8,0),B(2,0),C(0,4)三点,圆Q:x2+y2﹣2ay+a2﹣4=0.
(1)求圆P的方程;
(2)如果圆P和圆Q相外切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,﹣2cosx),
=(sinx,﹣2cosx), ![]() =(sinx+
=(sinx+ ![]() cosx,﹣cosx),x∈R.函数f(x)=
cosx,﹣cosx),x∈R.函数f(x)= ![]()
![]() .
.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2﹣6x+1与坐标轴的交点都在圆C上.
(Ⅰ)求圆C的方程;
(Ⅱ)若圆C与直线x﹣y+a=0交与A,B两点,且OA⊥OB,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设f(n)表示前n年的纯利润总和(f(n)=前n年的总收入﹣前n年的总支出﹣投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方法:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
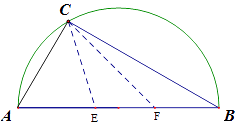
【题目】如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是 ![]() ,点E,F在直径AB上,且
,点E,F在直径AB上,且 ![]() .
. 
(1)若 ![]() ,求AE的长;
,求AE的长;
(2)设∠ACE=α,求该空地种植果树的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com