
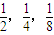 ,…中找出一个无穷等比的子数列(由原数列中部分项按原来次序排列的数列),使它所有项的和为
,…中找出一个无穷等比的子数列(由原数列中部分项按原来次序排列的数列),使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .  (|q|<1),根据已知的所有项的项的和得出首项与公比的关系式,由首项和公比都为
(|q|<1),根据已知的所有项的项的和得出首项与公比的关系式,由首项和公比都为 的次幂,通过代入得到首项与公比的值,进而表示出此子数列的通项公式.
的次幂,通过代入得到首项与公比的值,进而表示出此子数列的通项公式. ,得到
,得到 =
= ,即q=1-7a1,
,即q=1-7a1, 的次幂,
的次幂, ,q=
,q= ,
, .
.
 (|q|<1),等比数列的性质以及等比数列的通项公式,其中根据无穷数列的前n项的极限得出首项与公比的关系是解本题的关键.
(|q|<1),等比数列的性质以及等比数列的通项公式,其中根据无穷数列的前n项的极限得出首项与公比的关系是解本题的关键. 

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 7 |
| 1 |
| 8n |
| 1 |
| 8n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 7 |
| 1 |
| 8n |
| 1 |
| 8n |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 7 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市望江中学高三(上)第五次月考数学试卷(理科)(解析版) 题型:填空题
 ,
, ,
, ,…中找出一个无穷等比的子数列,使它所有项的和为
,…中找出一个无穷等比的子数列,使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市望江中学高三(上)第五次月考数学试卷(理科)(解析版) 题型:填空题
 ,
, ,
, ,…中找出一个无穷等比的子数列,使它所有项的和为
,…中找出一个无穷等比的子数列,使它所有项的和为 ,则此子数列的通项公式为 .
,则此子数列的通项公式为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com