
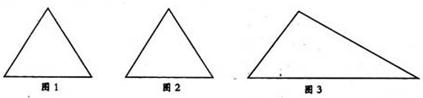
如图(1)、(2)给出两块相同的正三角形纸片,要求用其中一块剪拼成一个正三棱锥模型,另一块剪接成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图(1),图中(2),并作简要说明;(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;(3)如果给出的是一块任意三角形纸片,要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图(3)中,并作简要说明.

|
(1) 如图(1),沿正三角形三边中点连线折起,可拼得一个正三棱锥.如图(2),正三角形三个角剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的 ,有一组对角为直角.余下的部分按虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底.(2)设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱住的底面都是边长为1的正三角形,其面积为 ,有一组对角为直角.余下的部分按虚线折起,可成为一个缺上底的正三棱柱,而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底.(2)设给出正三角形纸片的边长为2,那么,正三棱锥与正三棱住的底面都是边长为1的正三角形,其面积为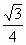 ,现在计算它们的高: ,现在计算它们的高: , , , ,
∴ 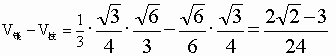 <0∴ <0∴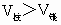 . .
(3) 如图(3),分别连结三角形的内心与各顶点,得到三条线段,再以这些线段的中点为顶点作三角形.以新三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可以拼成直棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱模型.本题改变了以住应用题建立一个数学模型,解决有关数据,本题要先设计剪拼出模型,然后计算,主要考查空间想象力,动手操作能力、探究能力和灵活运用所学知识解决现实问题和能力.这种题型有较大的自由度和思想空间,为学生提供了创新的天地,对学生的动手能力、逆向思维能力、语言表达能力等也有了更高的要求. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
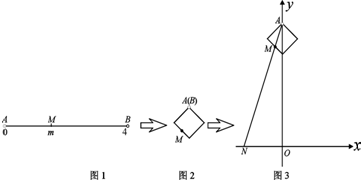 下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
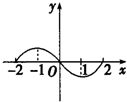 已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:
已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com