
【题目】如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙![]() 长为
长为![]() 米(2
米(2![]() ).
).
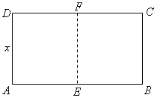
⑴用![]() 表示墙
表示墙![]() 的长;
的长;
⑵假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价![]() (元)表示为
(元)表示为![]() (米)的函数;
(米)的函数;
⑶当![]() 为何值时,墙壁的总造价最低?
为何值时,墙壁的总造价最低?
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
,![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]()
![]() ,
,![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
,![]() ,则
,则![]() 为单调函数.
为单调函数.
其中假命题为( )
A.① ③ B.② C.③④ D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在锐角△ABC中,两向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p与q是共线向量.
(1)求A的大小;
(2)求函数y=2sin2B+cos(![]() )取最大值时,角B的大小.
)取最大值时,角B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点![]() 的椭圆
的椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 为其右焦点.
为其右焦点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在平行于![]() 的直线
的直线![]() ,使得直线
,使得直线![]() 与椭圆
与椭圆![]() 有公共点,且直线
有公共点,且直线![]() 与
与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年的蔬菜销售收入均为50万元,设![]() 表示前
表示前![]() 年的纯利润总和(
年的纯利润总和(![]() =前
=前![]() 年的总收入
年的总收入![]() 前
前![]() 年的总支出
年的总支出![]() 投资额).
投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:
① 当年平均利润达到最大时,以48万元出售该厂;
② 当纯利润总和达到最大时,以16万元出售该厂,
问哪种方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)若![]() ,存在实数
,存在实数![]() ,对任意
,对任意![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据俄罗斯新罗西斯克2015年5月17日电 记者吴敏、郑文达报道:当地时间17日,参加中俄“海上联合-2015(Ⅰ)”军事演习的9艘舰艇抵达地中海预定海域,混编组成海上联合集群.接到命令后我军在港口M要将一件重要物品用小艇送到一艘正在航行的俄军轮船上,在小艇出发时,轮船位于港口M北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值并说明你的推理过程;
(3)是否存在v,使得小艇以v海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com