
【题目】某工厂生产甲,乙两种图画纸,计划每种图画纸的生产量不少于8t,已知生产甲种图画纸1t要用芦苇7t、黄麻3t、枫树5t;生产乙种图画纸1t要用芦苇3t、黄麻4t、枫树8 t.现在仓库内有芦苇300t、黄麻150t.枫树200t,试列出满足题意的不等式组.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在地面上同一地点观测远方匀速垂直上升的热气球,在上午10点整热气球的仰角是![]() ,到上午10点20分的仰角变成
,到上午10点20分的仰角变成![]() .请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
.请利用下表判断到上午11点整时,热气球的仰角最接近哪个度数( )
|
|
|
|
|
|
|
|
|
|
| 0.5 | 0.559 | 0.629 | 0.643 | 0.656 | 0.669 | 0.682 | 0.695 | 0.707 |
| 0.866 | 0.829 | 0.777 | 0.766 | 0.755 | 0.743 | 0.731 | 0.719 | 0.707 |
| 0.577 | 0.675 | 0.810 | 0.839 | 0.869 | 0.900 | 0.933 | 0.966 | 1.0 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ex(a∈R).其中e是自然对数的底数.
(1)讨论函数f(x)的单调性并求极值;
(2)令函数g(x)=f(x)+ex,若x∈[1,+∞)时,g(x)≥0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)
炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:

(1)据统计表明,![]() 之间具有线性相关关系,请用相关系数r加以说明(
之间具有线性相关关系,请用相关系数r加以说明(![]()
![]() ,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
,则认为y与x有较强的线性相关关系,否则认为没有较强的线性相关关系,r精确到0.001);
(2)建立y关于x的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题是否正确(正确的在括号内打“√”,错误的打“×”).
(1)![]() .(________)
.(________)
(2)![]() .(________)
.(________)
(3)![]() .(________)
.(________)
(4)![]() .(________)
.(________)
查看答案和解析>>
科目:高中数学 来源: 题型:
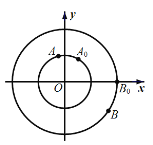
【题目】如图,点![]() 分别是圆心在原点,半径为
分别是圆心在原点,半径为![]() 和
和![]() 的圆上的动点.动点
的圆上的动点.动点![]() 从初始位置
从初始位置![]() 开始,按逆时针方向以角速度
开始,按逆时针方向以角速度![]() 作圆周运动,同时点
作圆周运动,同时点![]() 从初始位置
从初始位置![]() 开始,按顺时针方向以角速度
开始,按顺时针方向以角速度![]() 作圆周运动.记
作圆周运动.记![]() 时刻,点
时刻,点![]() 的纵坐标分别为
的纵坐标分别为![]() .
.
(Ⅰ)求![]() 时刻,
时刻,![]() 两点间的距离;
两点间的距离;
(Ⅱ)求![]() 关于时间
关于时间![]() 的函数关系式,并求当
的函数关系式,并求当![]() 时,这个函数的值域.
时,这个函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i的点.
(1)位于第四象限?
(2)位于第一、三象限?
(3)位于直线y=x上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P(万元)和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=![]() ,Q=
,Q=![]()
![]() .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com