(1)已知f(x)为一次函数,f[f(x)]=2x-1,求f(x)的解析式.
(2)函数y=f(x)是(-∞,+∞)上的奇函数,当x>0时f(x)=x2-2x-3,求函数y=f(x)的解析式.
(3)已知a,b为常数,若f(x)=x2+4x+3,f(ax+b)=x2+10x+24,求5a-b的值.
解:(1)设f(x)=ax+b,则f(f(x))=a(ax+b)+b=a
2x+ab+b
∵f[f(x)]=2x-1,∴a
2x+ab+b=2x-1
∴a
2=2且ab+b=-1,解得a=

,b=1-

或a=-

,b=1+

∴
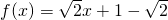
或
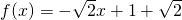
(2)∵y=f(x)是(-∞,+∞)上的奇函数,∴f(0)=0
下面求x<0时函数解析式
设x<0,则-x>0
∴f(-x)=(-x)
2-2(-x)-3=x
2+2x-3
∵y=f(x)是(-∞,+∞)上的奇函数
∴f(-x)=-f(x)
∴x<0时函数解析式f(x)=-x
2-2x+3
∴函数y=f(x)的解析式为
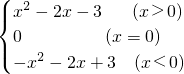
(3)∵f(x)=x
2+4x+3
∴f(ax+b)=(ax+b)
2+4(ax+b)+3=a
2x
2+(2ab+4a)x+b
2+4b+3=x
2+10x+24
∴
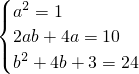
,解得
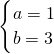
或
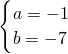
∴5a-b=2
分析:(1)运用待定系数法,设一次函数为f(x)=ax+b,代入已知后通过比较系数列方程求出a、b即可
(2)运用对称性求解析式,先确定f(0)=0,再设x<0,利用奇函数性质和x>0时f(x)=x
2-2x-3,求出x<0时函数解析式,最后将函数解析式合成分段函数
(3)运用待待定系数法,将ax+b代入f(x)=x
2+4x+3,化简后比较系数,列方程求出a、b即可
点评:本题考察了求函数解析式的方法,待定系数法,对称性法,配凑法等,解题时要归纳解题规律,认清形式,准确选择恰当方法解决问题.

 ,b=1-
,b=1- 或a=-
或a=- ,b=1+
,b=1+
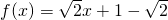 或
或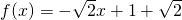
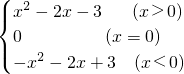
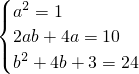 ,解得
,解得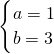 或
或