
分析 (1)由条件可得到$\left\{\begin{array}{l}{f(2)=4a+2b-1<0}\\{f(4)=16a+4b-3>0}\end{array}\right.$,这样即可得出4a-2b>0,从而得到2a>b;
(2)根据韦达定理可判断出x1,x2同号,从而可以得到两种情况:①-2<x1<0,-4<x2<-2,从而有$\left\{\begin{array}{l}{f(-4)>0}\\{f(-2)<0}\end{array}\right.$;②0<x1<2,2<x2<4,从而有$\left\{\begin{array}{l}{f(2)<0}\\{f(4)>0}\end{array}\right.$,这样便可得出b的取值范围.
解答 解:(1)证明:根据条件得,$\left\{\begin{array}{l}{f(2)<0}\\{f(4)>0}\end{array}\right.$;
即$\left\{\begin{array}{l}{4a+2b-1<0}&{①}\\{16a+4b-3>0}&{②}\end{array}\right.$;
∴①×(-3)+②得:4a-2b>0;
∴2a>b;
(2)∵${x}_{1}{x}_{2}=\frac{1}{a}>0$;
∴x1,x2同号;
由|x1|<2,|x1-x2|=2得,-2<x1<2,x1-x2=±2;
①若x1-x2=2,x2=x1-2∈(-4,0);
∴x1∈(-2,0),x2∈(-4,-2);
∴$\left\{\begin{array}{l}{f(-4)=16a-4b+5>0}\\{f(-2)=4a-2b+3<0}\end{array}\right.$;
∴$\left\{\begin{array}{l}{16a-4b+5>0}&{①}\\{-16a+8b-12>0}&{②}\end{array}\right.$;
①+②得,4b-7>0;
∴$b>\frac{7}{4}$;
②若x1-x2=-2,x2=x1+2∈(0,4);
∴x1∈(0,2),x2∈(2,4);
∴$\left\{\begin{array}{l}{f(2)=4a+2b-1<0}&{①}\\{f(4)=16a+4b-3>0}&{②}\end{array}\right.$;
∴①×(-4)+②得,-4b+1>0;
∴$b<\frac{1}{4}$;
∴综上得,b的取值范围为$(-∞,\frac{1}{4})∪(\frac{7}{4},+∞)$.
点评 考查韦达定理,绝对值不等式的解法,以及不等式的性质.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
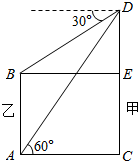 如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )
如图,甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是( )| A. | $\frac{40\sqrt{3}}{3}$ | B. | 20$\sqrt{3}$ | C. | 40 | D. | 10$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
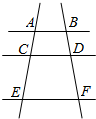
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com