练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知，将的图像向右平移个单位后，再保持纵坐标不变，横坐标变为原来的2倍，得到函数的图象.

    （1）求函数在上的值域及单调递增区间；

    （2）若，且，，求的面积.

    【答案】（1）值域为，单调递增区间为；（2）.

    【解析】

    （1）利用降幂公式和辅助角公式可得，结合图象变换可得的解析式，再利用正弦函数的性质可求在上的值域及单调递增区间.

    （2）先求出，，从而可求，再根据正弦定理求出，最后根据面积公式可求的面积.

    解：（1）

    ，

    则的图象向右平移个单位后，再保持纵坐标不变，横坐标变为原来的2倍，

    故可得，

    由，则，则，

    则的值域为.

    令，，

    则，由，则单调递增区间为.

    （2）因为，即可得，因为，故可得.

    由，求得，

    故可得.

    由正弦定理得，即，解得.

    又，

    故的面积.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知某种新型病毒的传染能力很强，给人们生产和生活带来很大的影响，所以创新研发疫苗成了当务之急.为此，某药企加大了研发投入，市场上这种新型冠状病毒的疫苗的研发费用（百万元）和销量（万盒）的统计数据如下：

    研发费用（百万元）

    2

    3

    6

    10

    13

    14

    销量（万盒）

    1

    1

    2

    2.5

    4

    4.5

    （1）根据上表中的数据，建立关于的线性回归方程（用分数表示）；

    （2）根据所求的回归方程，估计当研发费用为1600万元时，销售量为多少？

    参考公式：，.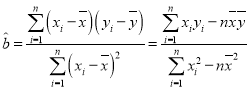

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，已知椭圆的离心率为，左右焦点分别是和，以为圆心，3为半径的圆与以为圆心，1为半径的圆相交，且交点在椭圆C上.

    （1）求椭圆C的方程.

    （2）设椭圆，P为椭圆C上任意一点，过点P的直线交椭圆E于A、B两点，射线OP交椭圆E于点Q.

    ①判断是否为定值？若是定值求出该定值，若不是定值说明理由.

    ②求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中共有8个球，其中有3个白球，5个黑球，这些球除颜色外完全相同．从袋中随机取出一球，如果取出白球，则把它放回袋中；如果取出黑球，则该黑球不再放回，并且另补一个白球放入袋中．重复上述过程次后，袋中白球的个数记为．

    （1）求随机变量的概率分布及数学期望；

    （2）求随机变量的数学期望关于的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）若，求的单调性和极值；

    （Ⅱ）若函数至少有1个零点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新冠肺炎疫情这只“黑天鹅”的出现，给经济运行带来明显影响，住宿餐饮、文体娱乐、交通运输、旅游等行业受疫情影响严重.随着复工复产的有序推动，我市某西餐厅推出线上促销活动：

    A套餐（在下列食品中6选3）

    西式面点：蔓越莓核桃包、南瓜芝土包、黑列巴、全麦吐司；

    中式面点：豆包、桂花糕

    B套餐：酱牛肉、老味烧鸡熟食类组合.

    复工复产后某一周两种套餐的日销售量（单位：份）如下：

    星期一

    星期二

    星期三

    星期四

    星期五

    星期六

    星期日

    A套餐

    11

    12

    14

    18

    22

    19

    23

    B套餐

    6

    13

    15

    15

    37

    20

    41

    （1）根据上面一周的销量，计算A套餐和B套餐的平均销量和方差，并根据所得数据评价两种套餐的销售情况；

    （2）若某顾客购买一份A套餐，求他所选的面点中至少一种中式面点的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线（为参数），直线 （为参数， ），直线与曲线相切于点，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系.

    （1）求曲线的极坐标方程及点的极坐标；

    （2）曲线的直角坐标方程为，直线的极坐标方程为，直线与曲线交于在，两点，记的面积为，的面积为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】算筹是在珠算发明以前我国独创并且有效的计算工具，为我国古代数学的发展做出了很大贡献.在算筹记数法中，以“纵式”和“横式”两种方式来表示数字，如下表：

    数字形式

    纵式

    横式

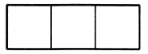
    表示多位数时，个位用纵式，十位用横式，百位用纵式，千位用横式，以此类推，遇零则置空，如图所示.如果把根算筹以适当的方式全部放入下面的表格中，那么可以表示的三位数的个数为______.

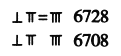
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其导函数为，函数，对任意，不等式恒成立.

    （1）求实数的值；

    （2）若，求证：.

    查看答案和解析>>

    同步练习册答案