
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 的斜率
的斜率![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 轴上是否存在点
轴上是否存在点![]() ,总有
,总有![]() ?若存在,求出点
?若存在,求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解了近五个月的实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
销量(万量) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买新能源汽车的消费者对补贴金额的心理预期值![]() 的方差
的方差![]() 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:①回归直线的斜率和截距的最小二乘估计公式分别为: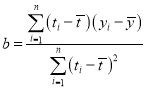 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
①3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值![]() 单位:
单位:![]() 与游玩时间
与游玩时间![]() 小时)满足关系式:
小时)满足关系式:![]() ;
;
②3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为![]() 即累积经验值不变);
即累积经验值不变);
③超过5小时为不健康时间,累积经验值开始损失,损失的经验值与不健康时间成正比例关系,比例系数为50.
⑴当![]() 时,写出累积经验值E与游玩时间t的函数关系式
时,写出累积经验值E与游玩时间t的函数关系式![]() ,并求出游玩6小时的累积经验值;
,并求出游玩6小时的累积经验值;
⑵该游戏厂商把累积经验值E与游玩时间t的比值称为“玩家愉悦指数”,记作![]() ;若
;若![]() ,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互变化、对称统一的形式美、和谐美.给出定义:能够将圆![]() (
(![]() 为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
为坐标原点)的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
①对于任意一个圆![]() ,其“优美函数”有无数个;
,其“优美函数”有无数个;
②函数![]() 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数![]() 可以同时是无数个圆的“优美函数”;
可以同时是无数个圆的“优美函数”;
④函数![]() 是“优美函数”的充要条件为函数
是“优美函数”的充要条件为函数![]() 的图象是中心对称图形.
的图象是中心对称图形.

A.①④B.①③④C.②③D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com