
【题目】(本题共12分)已知函数![]() .
.
(1)求函数![]() 的极值点;
的极值点;
(2)若f(x)≥x2+1在(0,2)上恒成立,求实数t的取值范围.
【答案】(1)当t≥0时,f(x)没有极值点;当t<0时,f(x)的极小值点为x=ln(-t),没有极大值点.
(2)![]()
【解析】试题分析:
(1)首先对函数![]() 求导,考虑到导函数含有参数
求导,考虑到导函数含有参数![]() ,对参数
,对参数![]() 大于等于0,和小于0两种情况进行讨论。
大于等于0,和小于0两种情况进行讨论。
(2)恒成立问题,首先利用参数分离,得到![]() ,再令
,再令![]() ,原问题转化为
,原问题转化为![]() ,从而求出参数
,从而求出参数![]() 的范围。
的范围。
试题解析:
(1)![]() ,
, ![]()
①当![]() 时,
时, ![]() ,
, ![]() 在R上单调递增,所以没有极值点。
在R上单调递增,所以没有极值点。
②当![]() 时,令
时,令![]() ,解得
,解得![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,
, ![]() 单调递增,所以
单调递增,所以![]() 为极小值点,没有极大值。
为极小值点,没有极大值。
(2)![]()
![]() 在
在![]() 上恒成立
上恒成立
![]() 在
在![]() 上恒成立
上恒成立
等价于: ![]() ,令
,令![]()
![]()
令![]() ,得
,得![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,
, ![]() 单调递增,所以
单调递增,所以![]()
![]() ,
,
所以![]() 的取值范围
的取值范围![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(Ⅰ)证明:CD⊥AE;
(Ⅱ)证明:PD⊥平面ABE;
(Ⅲ)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体A﹣BCD,则在四面体ABCD中,下列结论正确的是( ) 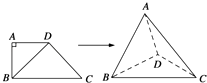
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com