
【题目】如图,在郊野公园的景观河的两岸,![]() 、
、![]() 是夹角为120°的两条岸边步道(长度均超过
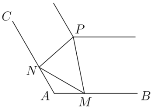
是夹角为120°的两条岸边步道(长度均超过![]() 千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台
千米),为方便市民观光游览,现准备在河道拐角处的另一侧建造一个观景台![]() ,在两条步道
,在两条步道![]() 、
、![]() 上分别设立游客上下点
上分别设立游客上下点![]() 、
、![]() ,从
,从![]() 、
、![]() 到观景台
到观景台![]() 建造两条游船观光线路
建造两条游船观光线路![]() 、
、![]() ,测得
,测得![]() 千米.
千米.
(1)求游客上下点![]() 、
、![]() 间的距离;
间的距离;
(2)若![]() ,设
,设![]() ,求两条观光线路
,求两条观光线路![]() 与
与![]() 之和关于
之和关于![]() 的表达式
的表达式![]() ,并求其最大值.
,并求其最大值.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】中国古代教育要求学生掌握“六艺”,即“礼、乐、射、御、书、数”.某校为弘扬中国传统文化,举行有关“六艺”的知识竞赛.甲、乙、丙三位同学进行了决赛.决赛规则:决赛共分![]() 场,每场比赛的第一名、第二名、第三名的得分分别为
场,每场比赛的第一名、第二名、第三名的得分分别为![]() ,选手最后得分为各场得分之和,决赛结果是甲最后得分为
,选手最后得分为各场得分之和,决赛结果是甲最后得分为![]() 分,乙和丙最后得分都为
分,乙和丙最后得分都为![]() 分,且乙在其中一场比赛中获得第一名,现有下列说法:
分,且乙在其中一场比赛中获得第一名,现有下列说法:
①每场比赛第一名得分![]() 分;
分;
②甲可能有一场比赛获得第二名;
③乙有四场比赛获得第三名;
④丙可能有一场比赛获得第一名.
则以上说法中正确的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:3x+4y+m=0,圆C:x2+y2-4x+2=0,则圆C的半径r=_____;若在圆C上存在两点A,B,在直线l上存在一点P,使得∠APB=90°,则实数m的取值范围是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将含有甲、乙、丙的6名医护人员平均分成两组到A、B两家医院参加“防疫救护”工作,则甲、乙至少有一人在A医院且甲、丙不在同一家医院参加“防疫救护”工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是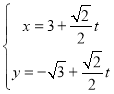 (t为参数),直线l与曲线C相交于A,B两点.
(t为参数),直线l与曲线C相交于A,B两点.
(1)求![]() 的长;
的长;
(2)求点![]() 到A,B两点的距离之积.
到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每
件该产品,且每件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检验方案:将产品每![]() 个(
个(![]() )一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或
)一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验一次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次数为
件该产品,记每件产品的平均检验次数为![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越大时,该方案越合理,即所需平均检验次数越少;
越大时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 的图象把圆
的图象把圆![]() 的面积两等分
的面积两等分
②![]() 是周期为
是周期为![]() 的函数
的函数
③函数![]() 在区间
在区间![]() 上有3个零点
上有3个零点
④函数![]() 在区间
在区间![]() 上单调递减
上单调递减
其中所有正确结论的编号是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数f(x)在[0,π]上的单调递减区间;
(2)在锐角△ABC的内角A,B,C所对边为a,b,c,已知f(A)=﹣1,a=2,求△ABC的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com