
【题目】如图,为了测量正在海面匀速行驶的某船的速度,在海岸上选取距离1千米的两个观察
点C、D,在某天10:00观察到该船在A处,此时测得∠ADC=30°,2分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,
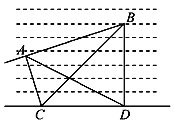
求该船航行的速度.
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是棱长为3的正方体,点
是棱长为3的正方体,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,(1)求证:
,(1)求证: ![]() 四点共面; (2)若点
四点共面; (2)若点![]() 在
在![]() 上,
上, ![]() ,点
,点![]() 在
在![]() 上,
上, ![]() ,垂足为
,垂足为![]() ,求证:
,求证: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成锐二面角大小,求
所成锐二面角大小,求![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年电子商务蓬勃发展,在2017年的“年货节”期间,一网络购物平台推销了![]() 三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了
三种商品,某网购者决定抢购这三种商品,假设该名网购者都参与了![]() 三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对
三种商品的抢购,抢购成功与否相互独立,且不重复抢购同一种商品,对![]() 三种商品的抢购成功的概率分别为
三种商品的抢购成功的概率分别为![]() ,已知三件商品都被抢购成功的概率为
,已知三件商品都被抢购成功的概率为![]() ,至少有一件商品被抢购成功的概率为
,至少有一件商品被抢购成功的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若购物平台准备对抢购成功的![]() 三件商品进行优惠减免活动,
三件商品进行优惠减免活动, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,
百元, ![]() 商品抢购成功减免
商品抢购成功减免![]() 百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
百元,求该名网购者获得减免的总金额(单位:百元)的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上. 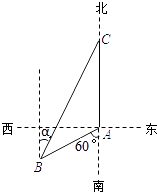
(1)求渔船甲的速度;
(2)求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足a1=2,a2=4(a3﹣a4),数列{bn}满足bn=3﹣2log2an .
(1)求数列{an}和{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)若λ>0,求对所有的正整数n都有2λ2﹣kλ+2>a2nbn成立的k的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于下列命题
①函数y=tanx在第一象限是增函数;
②函数y=cos2( ![]() ﹣x)是偶函数;
﹣x)是偶函数;
③函数y=4sin(2x﹣ ![]() )的一个对称中心是(
)的一个对称中心是( ![]() ,0);
,0);
④函数y=sin(x+ ![]() )在闭区间[﹣
)在闭区间[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com