
【题目】用数学归纳法证明:12﹣22+32﹣42+…+(﹣1)n﹣1n2=(﹣1)n﹣1 ![]() .
.
【答案】证明:①当n=1时,左边=1,右边=(﹣1)0![]() =1, 故:左边=右边,
=1, 故:左边=右边,
∴当n=1时,等式成立;
②假设n=k时,等式成立,即 12﹣22+32﹣42+…+(﹣1)k﹣1k2=(﹣1)k﹣1 ![]() .
.
那么12﹣22+32﹣42+…+(﹣1)k﹣1k2+(﹣1)k(k+1)2
=(﹣1)k﹣1 ![]() +(﹣1)k(k+1)2
+(﹣1)k(k+1)2
=(﹣1)k![]() (﹣k+2k+2)
(﹣k+2k+2)
=(﹣1)(k+1)﹣1![]()
即当n=k+1时,等式也成立.
根据①和②可知等式对任何n∈N+都成立
【解析】用数学归纳法证明问题的步骤是:第一步,验证当n=n0时命题成立,第二步假设当n=k时命题成立,那么再证明当n=k+1时命题也成立.关键是第二步中要充分用上归纳假设的结论.
【考点精析】根据题目的已知条件,利用数学归纳法的定义的相关知识可以得到问题的答案,需要掌握数学归纳法是证明关于正整数n的命题的一种方法.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为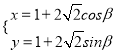 (
(![]() 为参数),在极坐标系中,直线
为参数),在极坐标系中,直线![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)写出曲线![]() 的直角坐标方程,并指出它是何种曲线;
的直角坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(4cosα,sinα),
=(4cosα,sinα), ![]() =(sinβ,4cosβ),
=(sinβ,4cosβ), ![]() =(cosβ,﹣4sinβ)
=(cosβ,﹣4sinβ)
(1)若 ![]() 与
与 ![]() ﹣2
﹣2 ![]() 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;
(2)若β∈(﹣ ![]() ],求|
],求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程 ![]() =﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
=﹣1表示的曲线即为函数y=f(x),有如下结论:( ) ①函数f(x)在R上单调递减;
②函数F(x)=4f(x)+3x不存在零点;
③函数y=f(x)的值域是R;
④若函数g(x)和f(x)的图象关于原点对称,则函数y=g(x)的图象就是方程 ![]() =﹣1确定的曲线.
=﹣1确定的曲线.
其中所有正确的命题序号是( )
A.①②
B.②③
C.①③④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆经过点![]() ,点
,点![]() 是椭圆上在第一象限的点,直线
是椭圆上在第一象限的点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)是否存在点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 平行?若存在,求出点
平行?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2x+ ![]() )+tan
)+tan ![]() cos2x.
cos2x.
(1)求f(x)的最小正周期及其图象的对称轴方程;
(2)求函数f(x)在区间(0, ![]() )上的值域.
)上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=x3与y=( ![]() )x﹣2的图象的交点为(x0 , y0),则x0所在的区间是( )
)x﹣2的图象的交点为(x0 , y0),则x0所在的区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com