
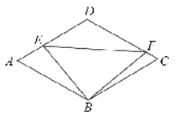
【题目】如图,郊外有一边长为200m的菱形池塘ABCD,塘边AB与AD的夹角为60°,拟架设三条网隔BE,BF,EF,把池塘分成几个不同区域,其中网隔BE与BF相互垂直,E,F两点分别在塘边AD和DC上,区域BEF为荷花种植区域.记∠ABE=![]() ,荷花种植区域的面积为Sm2.
,荷花种植区域的面积为Sm2.
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)求S的最小值.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】某二手车直卖网站对其所经营的一款品牌汽车的使用年数x与销售价格y(单位:万元,辆)进行了记录整理,得到如下数据:

(I)画散点图可以看出,z与x有很强的线性相关关系,请求出z与x的线性回归方程(回归系数![]() 精确到0.01);
精确到0.01);
(II)求y关于x的回归方程,并预测某辆该款汽车当使用年数为10年时售价约为多少.
参考公式:
参考数据:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产某种产品,为了提高生产效益,通过引进先进的生产技术和管理方式进行改革,并对改革后该产品的产量x(万件)与原材料消耗量y(吨)及100件产品中合格品与不合格品数量作了记录,以便和改革前作对照分析,以下是记录的数据:
表一:改革后产品的产量和相应的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二:改革前后定期抽查产品的合格数与不合格数
合格品的数量 | 不合格品的数量 | 合计 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合计 | 175 | 25 | 200 |
(1)请根据表一提供数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(2)已知改革前生产7万件产品需要6.5吨原材料,根据回归方程预测生产7万件产品能够节省多少原材料?
(3)请根据表二提供的数据,判断是否有90%的把握认为“改革前后生产的产品的合格率有差异”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A. [![]() ,+∞) B. [2,+∞) C. (0,
,+∞) B. [2,+∞) C. (0,![]() ] D. [0,
] D. [0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com