
【题目】已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)若函数![]() 的最小值为0,求实数
的最小值为0,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)令![]()
![]() ,当
,当![]() 时根据导数判断函数
时根据导数判断函数![]() 单调递增不符合题意,当
单调递增不符合题意,当![]() 时利用导数判断函数单调性从而求出最小值,根据最小值为0列出方程求解即可;(2)不等式化简为
时利用导数判断函数单调性从而求出最小值,根据最小值为0列出方程求解即可;(2)不等式化简为![]() ,则
,则![]() 对任意
对任意![]() 恒成立,令
恒成立,令![]() ,利用导数求出函数
,利用导数求出函数![]() 的最小值,根据不等式恒成立的条件即可求得a的值.
的最小值,根据不等式恒成立的条件即可求得a的值.
(1)![]() ,
,
所以![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,不合题意;
上单调递增,不合题意;
②当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,令
,令![]() ,则
,则![]() ,
,
因为![]() 时
时![]() ,
,![]() 时
时![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() ,所以由
,所以由![]() 知
知![]() ,解得
,解得![]() ,
,
即实数![]() 的值为
的值为![]() .
.
(2)因为![]() ,
,![]() 恒成立,所以
恒成立,所以![]() ,
,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
由(1)知,![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月1日起郑州市施行《郑州市城市生活垃圾分类管理办法》,郑州将正式进入城市生活垃圾分类时代.为了增强社区居民对垃圾分类知识的了解,积极参与到垃圾分类的行动中,某社区采用线下和线上相结合的方式开展了一次200名辖区成员参加的“垃圾分类有关知识”专题培训.为了了解参训成员对于线上培训、线下培训的满意程度,社区居委会随机选取了40名辖区成员,将他们分成两组,每组20人,分别对线上、线下两种培训进行满意度测评,根据辖区成员的评分(满分100分)绘制了如图所示的茎叶图.
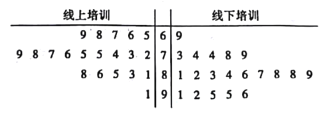
(1)根据茎叶图判断辖区成员对于线上、线下哪种培训的满意度更高,并说明理由.
(2)求这40名辖区成员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”“非常满意”两个等级.
分别视为“基本满意”“非常满意”两个等级.
(ⅰ)利用样本估计总体的思想,估算本次培训共有多少辖区成员对线上培训非常满意;
(ⅱ)根据茎叶图填写下面的列联表.
基本满意 | 非常满意 | 总计 | |
线上培训 | |||
线下培训 | |||
总计 |
并根据列联表判断能否有99.5%的把握认为辖区成员对两种培训方式的满意度有差异?
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7 | 10.828 |
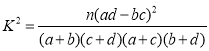 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率为
的焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某银行推销甲、乙两种理财产品(每种产品限购30万).每一件产品根据订单金额不同划分为:订单金额不低于20万为大额订单,低于20万为普通订单.银监部门随机调取购买这两种产品的客户各100户,对他们的订单进行分析,得到如图所示的频率分布直方图:
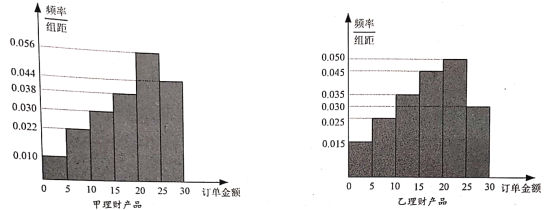
将此样本的频率估计视为总体的概率.购买一件甲产品,若是大额订单可盈利2万元,若是普通订单则亏损1万元,购买一件乙产品,若是大额订单可盈利1.5万元,若是普通订单则亏损0.5万元.
(1)记X为购买1件甲产品和1件乙产品所得的总利润,求随机变量X的数学期望;
(2)假设购买4件甲产品和4件乙产品所获得的利润相等.
(i)这4件甲产品和4件乙产品中各有大额订单多少件?
(ⅱ)这4件甲产品和4件乙产品中大额订单的概率哪个大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com