
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线l的参数方程为:
,直线l的参数方程为:![]() (t为参数),直线l与曲线C分别交于
(t为参数),直线l与曲线C分别交于![]() 两点.
两点.
(1)写出曲线C和直线l的普通方程;
(2)若点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,过
,过![]() 上一点
上一点![]() 的切线与(2)所求轨迹
的切线与(2)所求轨迹![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
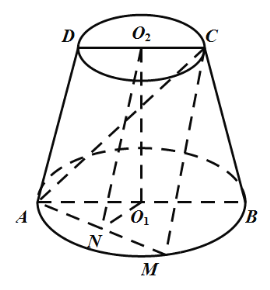
【题目】如图,在圆台![]() 中,平面
中,平面![]() 过上下底面的圆心
过上下底面的圆心![]() ,
,![]() ,点M在
,点M在![]() 上,N为
上,N为![]() 的中点,
的中点,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,
时,![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)若对任意![]() ,存在
,存在![]() 使
使![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() ,使得当
,使得当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
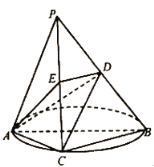
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在正常数
,若存在正常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立,我们称函数
成立,我们称函数![]() 为“
为“![]() 同比不减函数”.
同比不减函数”.
(1)求证:对任意正常数![]() ,
,![]() 都不是“
都不是“![]() 同比不减函数”;
同比不减函数”;
(2)若函数![]() 是“
是“![]() 同比不减函数”,求
同比不减函数”,求![]() 的取值范围;
的取值范围;
(3)是否存在正常数![]() ,使得函数
,使得函数![]() 为“
为“![]() 同比不减函数”,若存在,求
同比不减函数”,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{bn}的前n项和为Tn,且T4=4,b5=6.
(1)求数列{bn}的通项公式;
(2)若正整数n1,n2,…,nt,…满足5<n1<n2<…<nt,…且b3,b5,![]() ,
,![]() ,…,
,…,![]() ,…成等比数列,求数列{nt}的通项公式(t是正整数);
,…成等比数列,求数列{nt}的通项公式(t是正整数);
(3)给出命题:在公比不等于1的等比数列{an}中,前n项和为Sn,若am,am+2,am+1成等差数列,则Sm,Sm+2,Sm+1也成等差数列.试判断此命题的真假,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com