
【题目】已知圆![]() ,直线
,直线![]() 与圆
与圆![]() 相切,且交椭圆
相切,且交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆的半焦距,
是椭圆的半焦距, ![]() .
.
(1)求![]() 的值;
的值;
(2)![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(3)在(2)的条件下,设椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,
, ![]() ,动点
,动点![]() ,直线
,直线![]() ,
, ![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
, ![]() 两点,求线段
两点,求线段![]() 的长度的最小值.
的长度的最小值.
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1 , BB1的中点.
(1)画出过M,N,P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线;
(2)设过M,N,P三点的平面与B1C1交于Q,求PQ的长.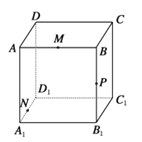
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司今年年初用98万元购进一艘渔船用于捕捞,第一年需要各种费用12万元.从第二年起包括维修费在内每年所需费用比上一年增加4万元.该船每年捕捞总收入50万元.
(1)问捕捞几年后总盈利最大,最大是多少?
(2)问捕捞几年后的平均利润最大,最大是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中
①函数f(x)=( ![]() )x的递减区间是(﹣∞,+∞)
)x的递减区间是(﹣∞,+∞)
②已知函数f(x)的定义域为(0,1),则函数f(x+1)的定义域为(1,2);
③已知(x,y)映射f下的象是(x+y,x﹣y),那么(4,2)在f下的原象是(3,1).
其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=x,g(x)= ![]()
D.f(x)=1,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com