
����Ŀ��ij�̳��ڴ����ڼ�涨���̳���������Ʒ����۵�![]() ���ۣ����˿����̳�������һ���������·��������Ӧ���Ľ�ȯ��
���ۣ����˿����̳�������һ���������·��������Ӧ���Ľ�ȯ��
���ѽ�Ԫ���ķ�Χ |
|
|
|
| �� |
��ý�ȯ�Ľ�Ԫ�� | 30 | 60 | 100 | 130 | �� |
�������������������˿��ڸ��̳�������Ի��˫���Żݣ����磺������Ϊ400Ԫ����Ʒ�������ѽ��Ϊ320Ԫ����õ��Żݶ�Ϊ��![]() Ԫ���蹺����Ʒ�õ����Ż��ʣ���������Ʒ��õ��Żݶ/����Ʒ��ۣ������ʣ�
Ԫ���蹺����Ʒ�õ����Ż��ʣ���������Ʒ��õ��Żݶ/����Ʒ��ۣ������ʣ�
��1��������һ�����Ϊ1000Ԫ����Ʒ���˿͵õ����Ż����Ƕ��٣�
��2�����ڱ����![]() ��Ԫ���ڵ���Ʒ���˿�����Ϊ����Ԫ����Ʒ���ɵõ���С��
��Ԫ���ڵ���Ʒ���˿�����Ϊ����Ԫ����Ʒ���ɵõ���С��![]() ���Ż��ʣ�
���Ż��ʣ�
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
���⿼����Dz���ʽ��Ӧ�����⣮�ڽ��ʱ��
��1��ֱ�Ӹ��ݹ�����Ʒ�õ����Ż���![]() �����ɻ������Ľ��
�����ɻ������Ľ��
��2�����ڱ����![]() ��
��![]() ��Ԫ
��Ԫ![]() �ڵ���Ʒ�������ѽ�����㣺
�ڵ���Ʒ�������ѽ�����㣺![]() ������Ҫ������ѽ�Ԫ
������Ҫ������ѽ�Ԫ![]() �ķ�Χ�������ۣ�Ȼ��ⲻ��ʽ�鼴�ɻ������Ľ��
�ķ�Χ�������ۣ�Ȼ��ⲻ��ʽ�鼴�ɻ������Ľ��
��1���������֪��![]() ��
��
�ʹ���һ�����Ϊ1000Ԫ����Ʒ���˿͵õ����Ż�����![]() ��
��
��2������Ʒ�ı��Ϊ![]() Ԫ��
Ԫ��
��![]() �����Ѷ
�����Ѷ![]() ��
��
����֪�ã���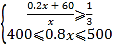 ����
����
����ʽ�飨���⣬����ʽ�飨�Ľ�Ϊ![]() ��
��
��ˣ����˿�������![]() ��
��![]() Ԫ�ڵ���Ʒʱ��
Ԫ�ڵ���Ʒʱ��
�ɵõ���С��![]() ���Ż��ʣ�
���Ż��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڸ��ⳤ��Ϊ2����������![]() �У�
�У� ![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��
��![]() ���е㣬
���е㣬 ![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣬���У�
�ϵĶ��㣬���У� ![]() ������
������![]() ����
����![]() .
.
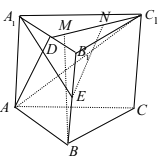
(1)֤��: ![]() ƽ��
ƽ��![]() ��
��
(2)��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ��������ֱ��
��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������α�![]() ��
��![]() ��
��![]() ������������������
������������������![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ���߹��㣬�õ��Ϊ
���߹��㣬�õ��Ϊ![]() �����Ƚ����ģ���
�����Ƚ����ģ���![]() ��ÿ���ڽǶ�С��120ʱ�����Ƚ����ĵ�P�����������ʣ�
��ÿ���ڽǶ�С��120ʱ�����Ƚ����ĵ�P�����������ʣ�
��1��![]() ����2�����Ƚ������ǵ��������������������֮����С�ĵ㣨Ҳ�������㣩�����������ʵ�
����2�����Ƚ������ǵ��������������������֮����С�ĵ㣨Ҳ�������㣩�����������ʵ�![]() ����СֵΪ_________
����СֵΪ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ļ����귽����
�ļ����귽����![]() .�Լ���Ϊƽ��ֱ������ϵ��ԭ�㣬����Ϊ
.�Լ���Ϊƽ��ֱ������ϵ��ԭ�㣬����Ϊ![]() ��������ᣬ����ƽ��ֱ������ϵ��ֱ��
��������ᣬ����ƽ��ֱ������ϵ��ֱ��![]() �IJ���������
�IJ���������![]() ��
��![]() ������.
������.
��������![]() �ļ����귽�̻�Ϊֱ�����귽�̣�
�ļ����귽�̻�Ϊֱ�����귽�̣�
������ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() ����б��
����б��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��ֱ��
��ֱ��![]() ��һ���㣬PA��PB��Բ
��һ���㣬PA��PB��Բ![]() ���������ߣ�A��BΪ�е㣬���ı���PACB�������Сֵ��2����
���������ߣ�A��BΪ�е㣬���ı���PACB�������Сֵ��2����![]() ��ֵ��
��ֵ��
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijȺ����˾�ͨ��ʱ�䣬��ָ�����ڸ�Ⱥ���г�Ա�Ӿ�ס�ص������ص�ƽ����ʱ��ij���ϰ���![]() �еij�Ա�����Լݻ���ʽͨ�ڣ�������ʾ����
�еij�Ա�����Լݻ���ʽͨ�ڣ�������ʾ����![]() ��
��![]() ��
��![]() ���ij�Ա�Լ�ʱ���Լ�Ⱥ����˾�ͨ��ʱ��Ϊ
���ij�Ա�Լ�ʱ���Լ�Ⱥ����˾�ͨ��ʱ��Ϊ ����λ�����ӣ���������Ⱥ����˾�ͨ��ʱ�䲻��
����λ�����ӣ���������Ⱥ����˾�ͨ��ʱ�䲻��![]() Ӱ�죬��Ϊ
Ӱ�죬��Ϊ![]() ���ӣ��Ը���������������ش��������⣺
���ӣ��Ը���������������ش��������⣺
��1����![]() ��ʲô��Χ��ʱ������Ⱥ����˾�ͨ��ʱ�������Լ�Ⱥ����˾�ͨ��ʱ�䣿
��ʲô��Χ��ʱ������Ⱥ����˾�ͨ��ʱ�������Լ�Ⱥ����˾�ͨ��ʱ�䣿
��2����õ��ϰ���![]() ���˾�ͨ��ʱ��
���˾�ͨ��ʱ��![]() �ı���ʽ������
�ı���ʽ������![]() �ĵ����ԣ���˵����ʵ�����壮
�ĵ����ԣ���˵����ʵ�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �����ֱ��
�����ֱ��![]() �������߽���
�������߽���![]() ��
��![]() ���㣬��Բ
���㣬��Բ![]() ����
����![]() ��
��![]() ���㣬��������ֱ������
���㣬��������ֱ������![]() ����
����![]() ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����R�ϵ�ż�������ҵ�x��0ʱ��f��x����x2��2x��
��1����f��0����f��f��1������ֵ��
��2������f��x���Ľ���ʽ��
��3��������x�ķ���f��x����m��0���ĸ���ͬ��ʵ���⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������һ����������״�ij��ڲ��������������DZ߳�Ϊ20cm�������Σ���Ϊ30cm������20cm�����Һ���ֽ���������бһ���Ƕ�![]() ��ͼ����������бʱ�����һ����ʼ���������ϣ�ͼ��������Ϊ�������ݽ��棩��
��ͼ����������бʱ�����һ����ʼ���������ϣ�ͼ��������Ϊ�������ݽ��棩��

��1��Ҫʹ��б�������ڵ���Һ�����������![]() �����ֵ�Ƕ��٣�
�����ֵ�Ƕ��٣�
��2������Ҫ����������![]() ����Һ����
����Һ����![]() ʱ����ʵ��Ҫ������˵�����ɣ�
ʱ����ʵ��Ҫ������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com