
分析 (Ⅰ)根据三角恒等变换化简cos2A-cos2B=$\sqrt{3}sinAcosA-\sqrt{3}sinBcosB$,求出A+B与C的值;
(Ⅱ)由余弦定理和基本不等式,即可求出周长a+b+c的取值范围.
解答 解:(Ⅰ)由cos2A-cos2B=$\sqrt{3}sinAcosA-\sqrt{3}sinBcosB$,
得$\frac{1+cos2A}{2}$-$\frac{1+cos2B}{2}$=$\frac{\sqrt{3}}{2}$sin 2A-$\frac{\sqrt{3}}{2}$sin 2B,…(2分)
即$\frac{\sqrt{3}}{2}$sin 2A-$\frac{1}{2}$cos 2A=$\frac{\sqrt{3}}{2}$sin 2B-$\frac{1}{2}$cos 2B,
所以sin(2A-$\frac{π}{6}$)=sin(2B-$\frac{π}{6}$),…(6分)
由a≠b,得A≠B,又A+B∈(0,π),
得2A-$\frac{π}{6}$+2B-$\frac{π}{6}$=π,
即A+B=$\frac{2π}{3}$,所以C=$\frac{π}{3}$;…(6分)
(Ⅱ)由余弦定理得:
c2=a2+b2-2ab•cosC3=a2+b2-ab=(a+b)2-3ab…(8分)
$>{(a+b)^2}-3\frac{{{{({a+b})}^2}}}{4}=\frac{{{{({a+b})}^2}}}{4}$,
则$a+b<2\sqrt{3}$,…(10分)
又$a+b>c=\sqrt{3}$,
$\sqrt{3}<a+b<2\sqrt{3}$,
$2\sqrt{3}<a+b+c<3\sqrt{3}$;
所以三角形周长的取值范围为$(2\sqrt{3},3\sqrt{3}\left.{\;})$.…(12分)
点评 本题考查了三角恒等变换以及余弦定理和基本不等式的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
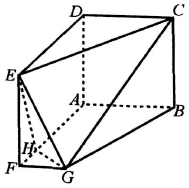 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
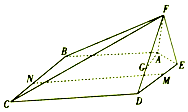 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3] | B. | [3,4) | C. | (4,5] | D. | [5,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com