


科目:高中数学 来源: 题型:
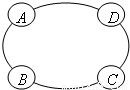
 15、如图是某汽车维修公司的维修点环形分布图.公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为
15、如图是某汽车维修公司的维修点环形分布图.公司在年初分配给A、B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为查看答案和解析>>
科目:高中数学 来源: 题型:
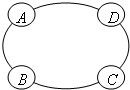
 1、如图是某汽车维修公司的维修点环形分布图.公司在年初分配给A,B,C,D四个维修点某种配件各50件.在使用前发现需将A,B,C,D四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为( )
1、如图是某汽车维修公司的维修点环形分布图.公司在年初分配给A,B,C,D四个维修点某种配件各50件.在使用前发现需将A,B,C,D四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为( )查看答案和解析>>
科目:高中数学 来源:广东 题型:单选题
| A.15 | B.16 | C.17 | D.18 |
查看答案和解析>>
科目:高中数学 来源:2011年湖北省武汉市武昌区高三五月调考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:11.1 分类加法计数原理与分步乘法计数原理1(理科)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com