
【题目】如图,在四棱锥中P﹣ABCD,底面ABCD为边长为 ![]() 的正方形,PA⊥BD.
的正方形,PA⊥BD. 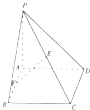
(1)求证:PB=PD;
(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小.
【答案】
(1)解:连接AC,BD交于点O,连结PO.
∵底面ABCD是正方形,
∴AC⊥BD,OB=OD.
又PA⊥BD,PA平面PAC,AC平面PAC,PA∩AC=A,
∴BD⊥平面PAC,∵PO平面PAC,
∴BD⊥PO.
又OB=OD,
∴PB=PD
(2)解:设PD的中点为Q,连接AQ,EQ,
则EQ∥CD,EQ= ![]() CD,又AF∥CD,AF=
CD,又AF∥CD,AF= ![]() =
= ![]() ,
,
∴EQ∥AF,EQ=AF,
∴四边形AQEF为平行四边形,∴EF∥AQ,
∵EF⊥平面PCD,∴AQ⊥平面PCD,
∴AQ⊥PD,∵Q是PD的中点,
∴AP=AD= ![]() .
.
∵AQ⊥平面PCD,∴AQ⊥CD,
又AD⊥CD,AQ∩AD=A,
∴CD⊥平面PAD,∴CD⊥PA.
又BD⊥PA,BD∩CD=D,
∴PA⊥平面ABCD.
以A为坐标原点,以AB,AD,AP为坐标轴建立如图所示的空间直角坐标系,
则B( ![]() ,0,0),P(0,0,
,0,0),P(0,0, ![]() ),A(0,0,0),Q(0,
),A(0,0,0),Q(0, ![]() ,
, ![]() ).
).
∴ ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,0,﹣
,0,﹣ ![]() ).
).
∵AQ⊥平面PCD,∴ ![]() 为平面PCD的一个法向量.
为平面PCD的一个法向量.
∴cos< ![]() >=
>= 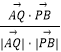 =﹣
=﹣ ![]() .
.
设直线PB与平面PCD所成角为θ,
则sinθ=|cos< ![]() >|=
>|= ![]() .
.
∴直线PB与平面PCD所成角为 ![]() .
.
【解析】(1)连接AC,BD交于点O,连结PO,则AC⊥BD,结合PA⊥BD得出BD⊥平面PAC,故而BD⊥PO,又O为BD的中点,得出OP为BD的中垂线,得出结论;(2)设PD的中点为Q,连接AQ,EQ,证明四边形AQEF是平行四边形,于是AQ⊥平面PCD,通过证明CD⊥平面PAD得出CD⊥PA,结合PA⊥BD得出PA⊥平面ABCD,以A为原点建立空间直角坐标系,则直线PB与平面PCD所成角的正弦值等于|cos< ![]() >|,从而得出线面角的大小.
>|,从而得出线面角的大小.
【考点精析】认真审题,首先需要了解空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则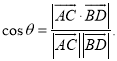 ).
).


科目:高中数学 来源: 题型:
【题目】已知 Sn是数列{an}的前n项和,且Sn=2an+n﹣4.
(1)求a1的值;
(2)若bn=an﹣1,试证明数列{bn}为等比数列;
(3)求数列{an}的通项公式,并证明: ![]() +
+ ![]() +…+
+…+ ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx﹣sin2x+
sinxcosx﹣sin2x+ ![]() .
.
(1)求f(x)的最小正周期值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ![]() ]上的最值及取最值时x的值.
]上的最值及取最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数f(x)=sin(2x+φ)(|φ|< ![]() )的图象上的所有点向左平移
)的图象上的所有点向左平移 ![]() 个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
A.y=g(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=g(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=g(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=g(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
(Ⅰ)在所给图中画出平面ABD1与平面B1EC的交线(不必说明理由);
(Ⅱ)证明:BD1∥平面B1EC;
(Ⅲ)求平面ABD1与平面B1EC所成锐二面角的大小.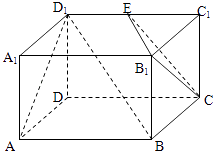
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA= ![]() ,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.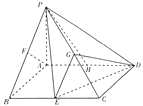
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=|2x﹣1|,定义f1(x)=x,fn+1(x)=f(fn(x)),已知函数g(x)=fm(x)﹣x有8个零点,则m的值为( )
A.8
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,已知定义在R上的函数
,已知定义在R上的函数![]() 在区间
在区间![]() 内有一个零点
内有一个零点![]() ,
, ![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,函数
,函数![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)求证:存在大于0的常数![]() ,使得对于任意的正整数
,使得对于任意的正整数![]() ,且
,且![]() 满足
满足![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com