
【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数之差为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据整除性确定员工人数可能情况,对应列方程,解方程组得结果.
设市场部和生产部的员工人数分别为x,y,不妨设y>x,
因为990不能被13整除,所以,两个部门人数之和:x+y≥51,
若51≤x+y≤100,则11(x+y)=990,得:x+y=90 (1)
因为1290不能被13整除,所以x,y不在同一区间[1,50],
从而1≤x≤50,51≤y≤100,
所以13x+11y=1290 (2)
解(1)(2)得:x=150,y=-60,不符合题意,
若x+y≥100,则9(x+y)=990,得:x+y=110 (3)
因为1290不能被11整除,所以1≤x≤50,51≤y
由13x+11y=1290 (4) 或13x+9y=1290 (5)
解(3)(4)得:x=40人,y=70人,
解(3)(5)得: y=35人,(舍)
所以,两部门人数之差为:y-x=30人,
故选:B.


科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式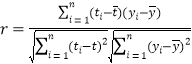
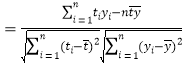 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: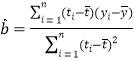
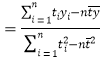 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在直线进行翻折,将
所在直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,
所在直线进行翻折,在翻折的过程中,
①点![]() 与点
与点![]() 在某一位置可能重合;②点
在某一位置可能重合;②点![]() 与点
与点![]() 的最大距离为
的最大距离为![]() ;
;
③直线![]() 与直线
与直线![]() 可能垂直; ④直线
可能垂直; ④直线![]() 与直线
与直线![]() 可能垂直.
可能垂直.
以上说法正确的个数为( )
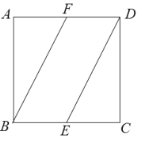
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
,![]() 两点.直线
两点.直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() (
(![]() ,
,![]() 与
与![]() 不重合)
不重合)
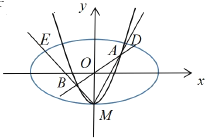
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的值;
的值;
(3)若![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C是平面内与两个定点![]() ,
,![]() 的距离之积等于常数
的距离之积等于常数![]() 的点的轨迹,给出下列三个结论:
的点的轨迹,给出下列三个结论:
①曲线过坐标原点;②曲线关于坐标原点对称;
③曲线关于横轴对称;④曲线关于纵轴对称;
⑤曲线关于![]() 对称;⑥若点P在曲线上,则
对称;⑥若点P在曲线上,则![]() 的面积不大于
的面积不大于![]() .
.
其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是由
是由![]()
![]() 个实数组成的
个实数组成的![]() 行
行![]() 列的数表,其中
列的数表,其中![]()
![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的实数,且
列的实数,且![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定义![]()
![]() 为第s行与第t行的积. 若对于任意
为第s行与第t行的积. 若对于任意![]() (
(![]() ),都有
),都有![]() ,则称数表
,则称数表![]() 为完美数表.
为完美数表.
(Ⅰ)当![]() 时,试写出一个符合条件的完美数表;
时,试写出一个符合条件的完美数表;
(Ⅱ)证明:不存在10行10列的完美数表;
(Ⅲ)设![]() 为
为![]() 行
行![]() 列的完美数表,且对于任意的
列的完美数表,且对于任意的![]() 和
和![]() ,都有
,都有![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .判定直线
.判定直线![]() 的斜率是否依次构成等差数列?并说明理由.
的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司年初以200万元购进一艘轮船,以每年40万元的价格出租给海运公司.轮船公司负责轮船的维护,第一年维护费为4万元,随着轮船的使用与磨损,以后每年的维护费比上一年多2万元,同时该轮船第![]() 年末可以以
年末可以以![]() 万元的价格出售.
万元的价格出售.
(1)写出轮船公司到第![]() 年末所得总利润
年末所得总利润![]() 万元关于
万元关于![]() 的函数解析式,并求
的函数解析式,并求![]() 的最大值;
的最大值;
(2)为使轮船公司年平均利润最大,轮船公司应在第几年末出售轮船?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com