练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱柱中，侧棱平面， ， ， ， ，点是的中点

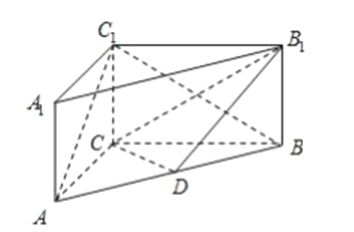
    （1）证明： 平面；

    （2）在线段上找一点，使得直线与所成角的为，求的值.

    【答案】（Ⅰ）见解析；（Ⅱ）

    【解析】试题分析：（1）证明线面平行,一般方法为利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找往往结合平几知识,如本题利用三角形中位线性质得线线平行,（2）研究线线角,一般可利用空间向量数量积求解,先根据题意建立恰当的空间直角坐标系,设立各点坐标,写出两直线方向向量,再根据向量数量积求夹角余弦值,最后根据线线角与向量夹角关系列关系式,求出的值．

    试题解析：（Ⅰ）证明：设与相交于，连结,

    是的中点， 是 的中点,

    ∥

    平面， 平面,∥平面

    （Ⅱ）建立空间直角坐标系， 为轴， 为轴， 为轴，

    设

    ，

    所以

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若{1，a， }={0，a2 ， a+b}，则a2005+b2005的值为（ ）
    A.0
    B.﹣1
    C.1
    D.1或﹣1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2017年5月13日第30届大连国际马拉松赛举行，某单位的10名跑友报名参加了半程马拉松、10公里健身跑、迷你马拉松3个项目(每人只报一项)，报名情况如下：

    项目

    半程马拉松

    10公里健身跑

    迷你马拉松

    人数

    2

    3

    5

    (其中：半程马拉松公里，迷你马拉松公里)

    (1)从10人中选出2人，求选出的两人赛程距离之差大于10公里的概率；

    (2)从10人中选出2人，设为选出的两人赛程距离之和，求随机变量的分布列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知．

    （Ⅰ）讨论函数的单调性；

    （Ⅱ）若函数在上有最小值，且最小值为，满足，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数

    （1）当时，求函数的单调区间；

    （2）令，其图象上任意一点处切线的斜率恒成立，求实数的取值范围.

    （3）当时，方程在区间内有唯一实数解，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】分别求出适合下列条件的直线方程：
    （Ⅰ）经过点且在x轴上的截距等于在y轴上截距的2倍；
    （Ⅱ）经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点，且和A（﹣3，1），B（5，7）等距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

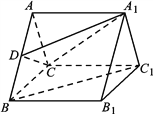
    【题目】如图，在三棱柱中，底面△ABC是等边三角形，侧面为正方形，且平面ABC， 为线段上的一点．

    (Ⅰ) 若∥平面A1CD，确定D的位置，并说明理由；

    (Ⅱ) 在(Ⅰ)的条件下，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的定义域为集合A，y=﹣x2+2x+2a的值域为B．
    （1）若a=2，求A∩B
    （2）若A∪B=R，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|（x+2）（x﹣5）＞0}，B={x|m≤x＜m+1}，且B（RA），则实数m的取值范围是 ．

    查看答案和解析>>

    同步练习册答案