
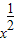 ,h(x)=x-2的大小关系是h(x)<g(x)<f(x);
,h(x)=x-2的大小关系是h(x)<g(x)<f(x);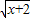 +
+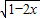 的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件.
的定义域为Q,则“x∈P”是“x∈Q”的充分不必要条件. 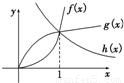
 },又由
},又由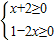
 },所以P?Q,所以x∈P是x∈Q的充分不必要条件.
},所以P?Q,所以x∈P是x∈Q的充分不必要条件.

 考前必练系列答案
考前必练系列答案科目:高中数学 来源:2011-2012学年安徽省高三第四次质量检测理科数学试卷 题型:填空题
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数
 恒成立”,则称
恒成立”,则称 为“完美函数”.给出以下四个函数
为“完美函数”.给出以下四个函数
① ②
②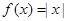 ③
③ ④
④
其中是“完美函数”的是 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年宁夏高三第一次月考理科数学试卷 题型:填空题
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
,
 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③ ④
④

其中是完美函数的序号是 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年吉林省高三上学期第二次理科数学月考试卷 题型:填空题
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
, 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③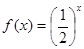 ④
④
其中是完美函数的序号是
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省四地六校联考高三上学期第二次月考理科数学卷 题型:选择题
若函数 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数 ,
, 恒成立”,则称
恒成立”,则称 为完美函数.给出以下四个函数
为完美函数.给出以下四个函数
① ②
② ③
③ ④
④
其中是完美函数的是( )
A.① B.② ③ C.①③ D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题![]() :“
:“![]() ”,命题
”,命题![]() :“
:“![]() ”,给出下列四个判断:①
”,给出下列四个判断:①![]() 是真命题,②
是真命题,②![]() 是真命题,③
是真命题,③![]() 是真命题,④
是真命题,④![]() 是真命题,其中正确的是( )
是真命题,其中正确的是( )
A. ② ④ B. ② ③
C. ③ ④ D. ① ② ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com