
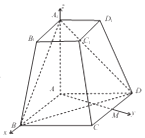
【题目】如图所示,在四棱台ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2. (Ⅰ)若M为CD中点,求证:AM⊥平面AA1B1B;
(Ⅱ)求直线DD1与平面A1BD所成角的正弦值.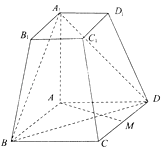
【答案】证明:(Ⅰ)∵四边形为菱形,∠BAD=120°,连结AC, ∴△ACD为等边三角形,
又∵M为CD中点,∴AM⊥CD,
由CD∥AB得,∴AM⊥AB,
∵AA1⊥底面ABCD,AM底面ABCD,∴AM⊥AA1 ,
又∵AB∩AA1=A,∴AM⊥平面AA1B1B
解:(Ⅱ)∵四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2,
∴DM=1, ![]() ,∠AMD=∠BAM=90°,
,∠AMD=∠BAM=90°,
又∵AA1⊥底面ABCD,
分别以AB,AM,AA1为x轴、y轴、z轴,建立如图所示的空间直角坐标系A﹣xyz,
则A1(0,0,2)、B(2,0,0)、 ![]() 、
、 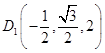 ,
,
∴ 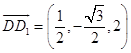 ,
, ![]() ,
, ![]() ,
,
设平面A1BD的一个法向量 ![]() ,
,
则有 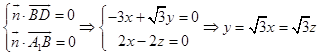 ,令x=1,则
,令x=1,则 ![]() ,
,
∴直线DD1与平面A1BD所成角θ的正弦值: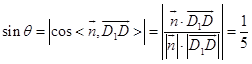 .
.
【解析】(Ⅰ)推导出AM⊥CD,AM⊥AB,AM⊥AA1 , 由此能证明AM⊥平面AA1B1B(Ⅱ)分别以AB,AM,AA1为x轴、y轴、z轴,建立如图所示的空间直角坐标系A﹣xyz,利用向量法能求出直线DD1与平面A1BD所成角θ的正弦值.
【考点精析】关于本题考查的直线与平面垂直的判定和空间角的异面直线所成的角,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则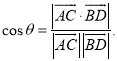 才能得出正确答案.
才能得出正确答案.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象向右平移 ![]() 个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|<
个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|< ![]() )的图象,则( )
)的图象,则( )
A.ω=2,φ=﹣ ![]()
B.ω=2,φ=﹣ ![]()
C.ω= ![]() ,φ=﹣
,φ=﹣ ![]()
D.ω= ![]() ,φ=﹣
,φ=﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
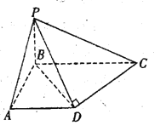
(1)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置;若不存在,说明理由.
上的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 的图像两相邻对称轴之间的距离是
的图像两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图像先向右平移
的图像先向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得函数
个单位,所得函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调区间;
的对称轴及单调区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆 ![]() 的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线 ![]() 与椭圆E有且仅有一个交点M. (Ⅰ)求椭圆E的方程;
与椭圆E有且仅有一个交点M. (Ⅰ)求椭圆E的方程;
(Ⅱ)设直线 ![]() 与y轴交于P,过点P的直线与椭圆E交于两不同点A,B,若λ|PM|2=|PA||PB|,求实数λ的取值范围.
与y轴交于P,过点P的直线与椭圆E交于两不同点A,B,若λ|PM|2=|PA||PB|,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 的图象大致为( )
的图象大致为( )
A.  B.
B. 
C.  D.
D. 
【答案】C
【解析】
由函数的解析式 ,当![]() 时,是函数的一个零点,属于排除A,B,
时,是函数的一个零点,属于排除A,B,
当x∈(0,1)时,cosx>0,![]() ,函数f(x) <0,函数的图象在x轴下方,排除D.
,函数f(x) <0,函数的图象在x轴下方,排除D.
本题选择C选项.
点睛:函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
【题型】单选题
【结束】
12
【题目】设![]() ,则
,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com