Question

【题目】在△ABC中，A，B的坐标分别是 ，点G是△ABC的重心，y轴上一点M满足GM∥AB，且|MC|=|MB|． （Ⅰ）求△ABC的顶点C的轨迹E的方程；
（Ⅱ）直线l：y=kx+m与轨迹E相交于P，Q两点，若在轨迹E上存在点R，使四边形OPRQ为平行四边形（其中O为坐标原点），求m的取值范围．

Answer 1

【答案】解：（Ⅰ）设C（x，y），∵点G是△ABC的重心， ∴G ，
∵y轴上一点M满足GM∥AB，∴ ．
∵|MC|=|MB|，
∴ ，
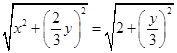化为 即为△ABC的顶点C的轨迹E的方程；
（Ⅱ）设P（x1 ， y1），Q（x2 ， y2），联立 ，化为（3+k2）x2+2kmx+m2﹣6=0，
由△＞0，化为 2k2﹣m2+6＞0，
∴ ， ．
∵四边形OPRQ为平行四边形，
∴ ，
∴R（x1+x2 ， y1+y2），y1+y2=k（x1+x2）+2m= ，
∴R ．
∵点R在椭圆上，
∴ =6，化为2m2=k2+3．
代入△＞0，可得m2＞0，
又2m2≥3，解得 或m ．
∴m的取值范围是 ∪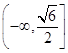
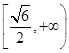
【解析】（Ⅰ）设C（x，y），由点G是△ABC的重心，可得G ，由y轴上一点M满足GM∥AB，可得 ．由|MC|=|MB|，利用两点之间的距离公式可得 ，即可得出；（Ⅱ）设P（x1 ， y1），Q（x2 ， y2），与椭圆方程联立化为（3+k2）x2+2kmx+m2﹣6=0，由△＞0，可得 2k2﹣m2+6＞0，由四边形OPRQ为平行四边形，可得 ，可得R（x1+x2 ， y1+y2），利用根与系数的关系可得R ．由点R在椭圆上，代入椭圆方程化为2m2=k2+3．结合△＞0，即可解出m的取值范围．