
【题目】过抛物线E:x2=2py(p>0)的焦点F作斜率率分别为k1 , k2的两条不同直线l1 , l2 , 且k1+k2=2.l1与E交于点A,B,l2与E交于C,D,以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在直线记为l.
(1)若k1>0,k2>0,证明: ![]() ;
;
(2)若点M到直线l的距离的最小值为 ![]() ,求抛物线E的方程.
,求抛物线E的方程.
【答案】
(1)解:由题意,抛物线E的焦点为 ![]() ,直线l1的方程为
,直线l1的方程为 ![]() .
.
由 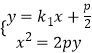 ,得
,得 ![]() .
.
设A,B两点的坐标分别为(x1,y1),(x2,y2),则x1,x2是上述方程的两个实数根.
从而x1+x2=2pk1, ![]() .
.
所以点M的坐标为 ![]() ,
, ![]() .
.
同理可得点N的坐标为 ![]() ,
, ![]() .
.
于是 ![]() .
.
由题设k1+k2=2,k1>0,k2>0,k1≠k2,所以0< ![]() .
.
故 ![]() .
.
(2)解:由抛物线的定义得 ![]() ,
, ![]() ,
,
所以 ![]() ,从而圆M的半径
,从而圆M的半径 ![]() .
.
故圆M的方程为 ![]() ,
,
化简得 ![]() .
.
同理可得圆N的方程为 ![]()
于是圆M,圆N的公共弦所在的直线l的方程为 ![]() .
.
又k2﹣k1≠0,k1+k2=2,则l的方程为x+2y=0.
因为p>0,所以点M到直线l的距离为
![]() =
= ![]() .
.
故当 ![]() 时,d取最小值
时,d取最小值 ![]() .由题设
.由题设 ![]() ,解得p=8.
,解得p=8.
故所求抛物线E的方程为x2=16y.
【解析】(1)由抛物线方程求出抛物线的焦点坐标,写出两条直线的方程,由两条直线方程和抛物线方程联立求出圆M和圆N的圆心M和N的坐标,求出向量 ![]() 和
和 ![]() 的坐标,求出数量积后转化为关于k1和k2的表达式,利用基本不等式放缩后可证得结论;(2)利用抛物线的定义求出圆M和圆N的直径,结合(1)中求出的圆M和圆N的圆心的坐标,写出两圆的方程,作差后得到两圆的公共弦所在直线方程,由点到直线的距离公式求出点M到直线l的距离,利用k1+k2=2转化为含有一个未知量的代数式,配方后求出最小值,由最小值等于
的坐标,求出数量积后转化为关于k1和k2的表达式,利用基本不等式放缩后可证得结论;(2)利用抛物线的定义求出圆M和圆N的直径,结合(1)中求出的圆M和圆N的圆心的坐标,写出两圆的方程,作差后得到两圆的公共弦所在直线方程,由点到直线的距离公式求出点M到直线l的距离,利用k1+k2=2转化为含有一个未知量的代数式,配方后求出最小值,由最小值等于 ![]() 求出p的值,则抛物线E的方程可求.
求出p的值,则抛物线E的方程可求.


科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中, ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央电视台播出的《朗读者》节目,受到广大人民群众的喜爱.随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获准匪浅,现从观看节目的观众中随机统计了4位观众的周均阅读学习经典的知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为50岁观众周均学习阅读经典知识的时间.
,并预测年龄为50岁观众周均学习阅读经典知识的时间.
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com