
分析 (1)由已知可得圆心C的轨迹是以F为焦点,以l为准线的抛物线,进而得到答案.
(2)首先由于过点M(m,0)的直线与开口向右的抛物线有两个交点A、B,则设该直线的方程为x=ty+m(包括无斜率的直线);然后与抛物线方程联立方程组,进而通过消元转化为一元二次方程;再根据韦达定理及向量的数量积公式,实现$\overrightarrow{FA}$•$\overrightarrow{FB}$<0的等价转化;最后通过m、t的不等式求出m的取值范围
解答 解:(1)∵动圆过定点F(1,0)且与定直线l:x=-1相切.
故圆心到点F(1,0)和直线l:x=-1的距离相等,
故圆心C的轨迹是以F为焦点,以l为准线的抛物线,
故动圆圆心C的轨迹方程这y2=4x;
(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).
设l的方程为x=ty+m,由$\left\{\begin{array}{l}x=ty+m\\{y}^{2}=4x\end{array}\right.$得y2-4ty-4m=0,△=16(t2+m)>0,
于是y1+y2=4t,y1•y2=-4m,①
又$\overrightarrow{FA}$=(x1-1,y1),$\overrightarrow{FB}$=(x2-1,y2),
∵$\overrightarrow{FA}$•$\overrightarrow{FB}$<0?(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+y1y2<0②
又x=$\frac{1}{4}$y2,于是不等式②等价于$\frac{1}{4}$y12•$\frac{1}{4}$y22+y1y2-($\frac{1}{4}$y12+$\frac{1}{4}$y22)+1<0
由①式,不等式③等价于m2-6m+1<4t2④
对任意实数t,4t2的最小值为0,所以不等式④对于一切t成立等价于m2-6m+1<0,
解得3-2$\sqrt{2}$<m<3+2$\sqrt{2}$,
由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有有$\overrightarrow{FA}$•$\overrightarrow{FB}$<0,
则m的取值范围是(3-2$\sqrt{2}$,3+2$\sqrt{2}$)
点评 本题着重考查了一元二次方程根与系数的关系、直线与抛物线的位置关系和向量数量积运算等知识,同时考查了逻辑思维能力、计算能力和转化化归的数学思想等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | x0=2 | B. | f(x0)=2 | C. | f′(x0)=2 | D. | $\frac{{y}_{0}}{{x}_{0}}$=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{5}{9}$) | C. | ($\frac{1}{2}$,$\frac{5}{9}$) | D. | ($\frac{5}{9}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
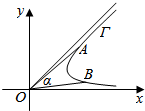 如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )
如图,在平面直角坐标系xOy中,对于曲线Γ,若存在以O为顶点的角α,使得α≥∠AOB对于曲线π上的任意两个不同的点A,B恒成立,则称角α为曲线的相对于点O的“渐近角”并称其中最小的“渐近角”为曲线Γ的相对于点O的“望角”.已知曲线C:y=$\left\{\begin{array}{l}{2x{e}^{x-1}+2,x>0}\\{\frac{\sqrt{36+25{x}^{2}}}{3},x≤0}\end{array}\right.$(其中e=2.71828…是自然对数的底数),则曲线C的相对于点O的“望角”为( )| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com