
【题目】一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
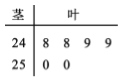
(Ⅰ)求这箱饮料的平均容量和容量的中位数;
(Ⅱ)如果从这箱饮料中随机取出2听饮用,求取到的2听饮料中至少有1听的容量为250ml的概率
【答案】(Ⅰ)根据平均数计算公式得饮料的平均容量为![]() ,中位数为中间两个数的平均值:
,中位数为中间两个数的平均值:![]() (Ⅱ)先利用枚举法确定从这6听饮料中随机抽取2听的所有可能结果,共有15种,其中取到的2听饮料容量都不为250ml的种数有6种,因此取到的2听饮料中至少有1听的容量为250ml的有9种,故根据古典概型概率公式得
(Ⅱ)先利用枚举法确定从这6听饮料中随机抽取2听的所有可能结果,共有15种,其中取到的2听饮料容量都不为250ml的种数有6种,因此取到的2听饮料中至少有1听的容量为250ml的有9种,故根据古典概型概率公式得![]()
【解析】
试题分析:(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
试题解析:(Ⅰ)由茎叶图知,这箱饮料的平均容量为![]() .
.
容量的中位数为![]() .…………………………………………4分
.…………………………………………4分
(Ⅱ)把每听饮料标上号码,其中容量为248ml,249ml的4听分别记作:1,2,3,4,容量为250ml的2听分别记作:![]() ,
,![]() .抽取2听饮料,得到的两个标记分别记为
.抽取2听饮料,得到的两个标记分别记为![]() 和
和![]() ,则
,则![]() 表示一次抽取的结果,即基本事件,从这6听饮料中随机抽取2听的所有可能结果有:
表示一次抽取的结果,即基本事件,从这6听饮料中随机抽取2听的所有可能结果有:
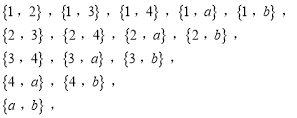
共计15种,即事件总数为15.
其中含有![]() 或
或![]() 的抽取结果恰有9种,即“随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml”的基本事件个数为9.
的抽取结果恰有9种,即“随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml”的基本事件个数为9.
所以从这箱饮料中随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml的概率为![]() .……12分
.……12分


科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三条边长,则下列结论中正确的是( )
的三条边长,则下列结论中正确的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三条边
不能构成一个三角形的三条边
②对一切![]() ,都有
,都有![]()
③若![]() 为钝角三角形,则存在
为钝角三角形,则存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
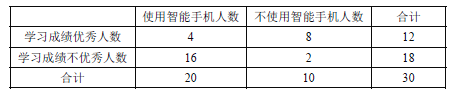
参考数据:

参考公式: 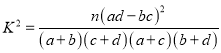 ,其中
,其中![]()
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为![]() 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为![]() 组,计划从
组,计划从![]() 组推选的2人和
组推选的2人和![]() 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自![]() 、
、![]() 两组的概率.
两组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高二年段的男生进行体检,现将高二男生的体重![]() 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组
数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组![]() 的人数为200.根据一般标准,高二男生体重超过
的人数为200.根据一般标准,高二男生体重超过![]() 属于偏胖,低于
属于偏胖,低于![]() 属于偏瘦.观察图形的信息,回答下列问题:
属于偏瘦.观察图形的信息,回答下列问题:
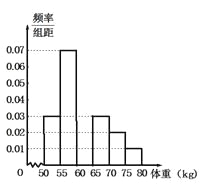
(1)求体重在![]() 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;
(2)用分层抽样的方法从偏胖的学生中抽取![]() 人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了四个类比推理:
(1)由“若![]() 则
则![]() ”类比推出“若
”类比推出“若![]() 为三个向量则
为三个向量则![]() ”;
”;
(2)“a,b为实数,![]() 则a=b=0”类比推出“
则a=b=0”类比推出“![]() 为复数,若
为复数,若![]() ”
”
(3)“在平面内,三角形的两边之和大于第三边”类比推出“在空间中,四面体的任意三个面的面积之和大于第四个面的面积”
(4)“在平面内,过不在同一条直线上的三个点有且只有一个圆”类比推出“在空间中,过不在同一个平面上的四个点有且只有一个球”.
上述四个推理中,结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,两焦点分别为
,两焦点分别为![]() ,过
,过![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求弦长
两点,求弦长![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件A:“取出的2件产品中至多有1件是二等品”,其概率P(A)=0.96.
(1)求从该批产品中任取1件是二等品的概率p.
(2)若该批产品共100件,从中无放回抽取2件产品,ξ表示取出的2件产品中二等品的件数.求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦; q:球心与小圆截面圆心的连线垂直于截面.
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等.
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径).
④p:圆的面积为S=![]() R·πd(R,d是圆的半径与直径); q:球的体积为V=
R·πd(R,d是圆的半径与直径); q:球的体积为V=![]() R·πd2(R,d是球的半径与直径).
R·πd2(R,d是球的半径与直径).
则上面的四组命题中,其中类比得到的q是真命题的有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com