
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)讨论函数![]() 的单调性.
的单调性.
(2)是否存在正实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() 时,值域也为
时,值域也为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)答案不唯一,具体见解析(2)存在;![]()
【解析】
(1)先对函数![]() 进行求导,根据已知条件在
进行求导,根据已知条件在![]() 处的切线方程为
处的切线方程为![]() 可求出
可求出![]() ,
,![]() ,即得到
,即得到![]() ,再对
,再对![]() 进行求导,对参数
进行求导,对参数![]() 进行讨论即可.
进行讨论即可.
(2)先假设存在符合题意的正实数![]() ,再对
,再对![]() 进行求导,可得到它的单调性以及单调区间,从而可求得
进行求导,可得到它的单调性以及单调区间,从而可求得![]() 的最小值大于或等于零即可.
的最小值大于或等于零即可.
解:(1)∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() ,得
,得![]() .
.
令![]() ,得
,得![]() ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)假设存在符合题意的正实数![]() ,
,
由![]() ,得
,得![]() .
.
∵![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 上单调递增.
上单调递增.
∵![]() ,且当
,且当![]() 时,
时,![]() ,
,
∴存在唯一的实数![]() ,使得
,使得![]() ,即
,即![]() ①,
①,
∴当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴![]() .
.
由![]() ,得
,得![]() ,
,
∴![]()
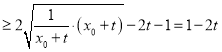 .
.
当且仅当![]() 时取等号,由
时取等号,由![]() ,得
,得![]() ,此时
,此时![]() ,
,
把![]() ,
,![]() 代入①也成立.
代入①也成立.
故存在正实数![]() ,使得
,使得![]() 定义域为
定义域为![]() 时,值域也为
时,值域也为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣(3a﹣2)x2﹣8x+12a+7,g(x)=lnx,记h(x)=min{f(x),g(x)},若h(x)至少有三个零点,则实数a的取值范围是( )
A.(﹣∞,![]() )B.(
)B.(![]() ,+∞)C.[
,+∞)C.[![]() ,
,![]() )D.[
)D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某摄影协会在2019年10月举办了主题“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头,记录了国强民富的幸福生活,向祖国母亲70岁的生日献了一份厚礼.摄影协会收到了来自社会各界的大量作品,从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:
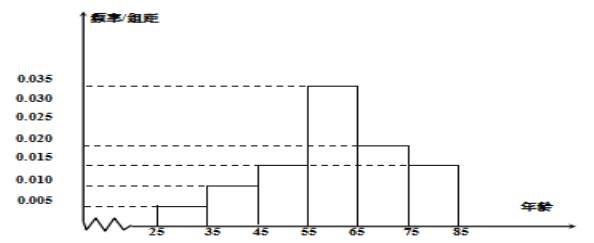
(1)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
(ii)摄影协会从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.
的人数是Y,求变量Y的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是矩形
是矩形![]() 内(含边界)的动点,且
内(含边界)的动点,且![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .记点
.记点![]() 的轨迹长度为
的轨迹长度为![]() ,则
,则![]() ______;当三棱锥
______;当三棱锥![]() 的体积最小时,三棱锥
的体积最小时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线上任意两点![]()
![]() 处的切线交于点
处的切线交于点![]() ,称
,称![]() 为“阿基米德三角形”.当线段
为“阿基米德三角形”.当线段![]() 经过抛物线焦点
经过抛物线焦点![]() 时,
时,![]() 具有以下特征:①
具有以下特征:①![]() 点必在抛物线的准线上;②
点必在抛物线的准线上;②![]() 为直角三角形,且
为直角三角形,且![]() ;③
;③![]() .若经过抛物线
.若经过抛物线![]() 焦点的一条弦为
焦点的一条弦为![]() ,阿基米德三角形为
,阿基米德三角形为![]() ,且点
,且点![]() 的纵坐标为4,则直线
的纵坐标为4,则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为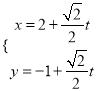 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com