
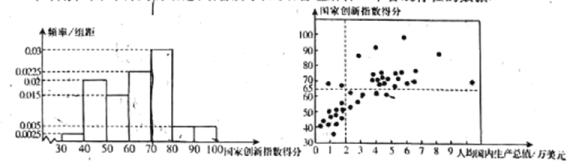
【题目】国家创新指数是反映一个国家科学技术和创新竞争力的综合指数.对国家创新指数得分排名前40的国家的有关数据进行收集.整理、描述和分析.下面给出了部分信息:
a.国家创新指数得分的频率分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
b.国家创新指数得分在![]() 这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
这一组的是:61.7,62.4,63.6,65.9,66.4,68.5,69.1,69.3,69.5.
c.40个国家的人均国内生产总值(万美元)和国家创新指数得分情况统计图:
d.中国的国家创新指数得分为69.5,人均国内生产总值9960美元.
(以上数据来源于《国家创新指数报告(2018)》)
根据以上信息,解答下列问题:
(1)中国的国家创新指数得分排名世界第几?
(2)是否有99.9%的把握认为“人均国内生产总值影响国家创新指数得分”?
(3)用(1)(2)得到的结论,结合所学知识.合理解释d中客观存在的数据.
附: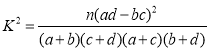 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)17;(2)有99.9%的把握认为“人均国内生产总值影响国家创新指数得分”;(3)见解析.
【解析】
(1)由题意可得在![]() 的频率为
的频率为![]() ,可得中国的国家创新指数得分排名;
,可得中国的国家创新指数得分排名;
(2)列出40个国家的人均国内生产总值和国家创新指数得分情况统计图可得![]() 列联表,
列联表,
计算![]() 的值后结合表格进行判断可得答案;
的值后结合表格进行判断可得答案;
(3)用(1)(2)得到的结论,可得“人均国内生产总值与国家创新指数得分成线性相关关系”,解释为:“中国特色社会主义制度的优越性,能够集中社会力量办大事”.
解:(1)由国家创新指数得分的频率分布直方图可得“国家创新指数得分”
在![]() 的频率为
的频率为![]() .
.
因此,中国的国家创新指数得分排名为![]() .
.
(2)由40个国家的人均国内生产总值和国家创新指数得分情况统计图可得![]() 列联表:
列联表:
人均国内生产总值 | 人均国内生产总值 | |
国家创新指数得分 | 2 | 20 |
国家创新指数得分 | 12 | 6 |
由![]() 列联表可得
列联表可得![]() .
.
由于![]() ,
,
故有99.9%的把握认为“人均国内生产总值影响国家创新指数得分”.
(3)答:(2)的结论说明,“人均国内生产总值与国家创新指数得分成线性相关关系”.事实上,我国的人均国内生产总值并不高,但是我国的国家创新指数相对比较高,恰恰说明了“中国特色社会主义制度的优越性,能够集中社会力量办大事”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)若![]() 的定义域为
的定义域为![]() ,判断
,判断![]() 的单调性,并加以说明;
的单调性,并加以说明;
(2)当![]() 时,是否存在
时,是否存在![]() ,
,![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求
,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
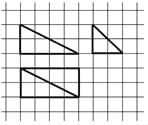
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的右焦点为F(1,0),且点P
(a>b>0)的右焦点为F(1,0),且点P![]() 在椭圆C上,O为坐标原点.
在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() ,
,![]() 在圆上且分别在
在圆上且分别在![]() 的两侧,其中
的两侧,其中![]() ,
,![]() .现将其沿
.现将其沿![]() 折起使得二面角
折起使得二面角![]() 为直二面角,则下列说法不正确的是( )
为直二面角,则下列说法不正确的是( )
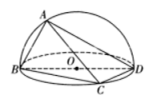
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一个球面上
在同一个球面上
B.当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
C.![]() 与
与![]() 是异面直线且不垂直
是异面直线且不垂直
D.存在一个位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点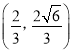
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com