
���� ֱ�������оٷ���ʾ��1����2����3����4����6����7����8����������������ʾ��5����
��� �⣺��1���й�����������ɫ��ȫ�������ɵļ������оٷ���ʾΪ��{��ɫ����ɫ}��
��2����������ߵ�ɽ�������ɵļ������оٷ���ʾΪ��{���������}��
��3������0����С��20����ż����ȫ�������ɵļ������оٷ���ʾΪ��{2��4��6��8��10��12��14��16��18}��
��4������0.9����С��3.9����Ȼ����ȫ�������ɵļ������оٷ���ʾΪ��{1��2��3}��
��5����3����1��������ȫ�������ɵļ�������������ʾΪ��{x|x=3n+1��n��N}��
��6��15����������ȫ�������ɵļ������оٷ���ʾΪ��{1��3��5��15}��
��7������ֵ����2��ʵ����ȫ�������ɵļ������оٷ���ʾΪ��{2��-2}��
��8��9��ƽ������ȫ�������ɵļ������оٷ���ʾΪ��{3��-3}��
���� ���⿼�鼯�ϵı�ʾ���������оٷ�����������ʾ���ϵĶ��壬�ѶȲ������ڻ����⣮


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ad+bc=0 | B�� | ac+bd=0 | C�� | ac=bd | D�� | ad=bc |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4$\sqrt{ab}$ | B�� | a+b+2$\sqrt{ab}$ | C�� | 2��a+b�� | D�� | ���Ͼ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 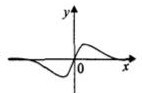 | B�� | 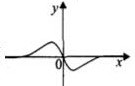 | C�� | 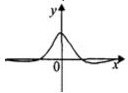 | D�� | 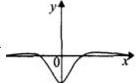 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{\sqrt{2}}{2}$ | B�� | -$\frac{4\sqrt{2}}{7}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{4\sqrt{2}}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com