
【题目】已知数列{an}是以d为公差的等差数列,{bn}数列是以q为公比的等比数列.
(1)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<a1003+5b2﹣2010,求整数q的值;
(2)在(1)的条件下,试问数列中是否存在一项bk,使得bk恰好可以表示为该数列中连续p(p∈N,p≥2)项的和?请说明理由;
(3)若b1=ar,b2=as≠ar,b3=at(其中t>s>r,且(s﹣r)是(t﹣r)的约数),求证:数列{bn}中每一项都是数列{an}中的项.
【答案】(1)2;(2)不存在;(3)详见解析.
【解析】
(1)先求an=2n,利用等比数列得![]() 的不等式求解即可;(2)反证法推得矛盾即可;(3)由b1=ar,得
的不等式求解即可;(2)反证法推得矛盾即可;(3)由b1=ar,得![]() ,进而
,进而![]() 得q是整数,且q≥2,再证明对于数列中任一项bi (i>3)一定是数列{an}的项即可
得q是整数,且q≥2,再证明对于数列中任一项bi (i>3)一定是数列{an}的项即可
(1)由题意知,an=2n,bn=2qn﹣1,所以由S3<a1003+5b2﹣2010,
可得到b1+b2+b3<a1003+5b2﹣2010b1﹣4b2+b3<2006﹣2010q2﹣4q+3<0.
解得1<q<3,又q为整数,所以q=2;
(2)假设数列{bn}中存在一项bk,满足bk=bm+bm+1+bm+2++bm+p﹣1,
因为bn=2n,∴bk>bm+p﹣12k>2m+p﹣1k>m+p﹣1k≥m+p(*)
又![]()
=2m+p﹣2m<2m+p,所以k<m+p,此与(*)式矛盾.
所以,这样的项bk不存在;
(3)由b1=ar,得b2=b1q=arq=as=ar+(s﹣r)d,
则![]()
又![]() ,
,
从而![]() ,
,
因为as≠arb1≠b2,所以q≠1,又ar≠0,
故![]() .又t>s>r,且(s﹣r)是(t﹣r)的约数,
.又t>s>r,且(s﹣r)是(t﹣r)的约数,
所以q是整数,且q≥2,
对于数列中任一项bi(这里只要讨论i>3的情形),
有bi=arqi﹣1=ar+ar(qi﹣1﹣1)
=ar+ar(q﹣1)(1+q+q2+![]() +qi﹣2)
+qi﹣2)
=ar+d(s﹣r)(1+q+q2+![]() +qi﹣2)
+qi﹣2)
=ar+[((s﹣r)(1+q+q2+![]() +qi﹣2)+1)﹣1]d,
+qi﹣2)+1)﹣1]d,
由于(s﹣r)(1+q+q2+![]() +qi﹣2)+1是正整数,所以bi一定是数列{an}的项.
+qi﹣2)+1是正整数,所以bi一定是数列{an}的项.
故得证.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的各项都是正数,若对于任意的正整数
的各项都是正数,若对于任意的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比数列,则称函数
成等比数列,则称函数![]() 为“
为“![]() 型”数列.
型”数列.
(1)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”数列,且
型”数列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”数列,又是“
型”数列,又是“![]() 型”数列,求证:数列
型”数列,求证:数列![]() 是等比数列.
是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
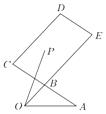
【题目】如图,B是AC的中点,![]() ,P是平行四边形BCDE内(含边界)的一点,且
,P是平行四边形BCDE内(含边界)的一点,且![]() .有以下结论:
.有以下结论:
①当x=0时,y∈[2,3];
②当P是线段CE的中点时,![]() ;
;
③若x+y为定值1,则在平面直角坐标系中,点P的轨迹是一条线段;
④x﹣y的最大值为﹣1;
其中你认为正确的所有结论的序号为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为整数的无穷数列![]() 满足:
满足:![]() ,且对所有
,且对所有![]() ,
,![]() 均成立.
均成立.
(1)写出![]() 的所有可能值(不需要写计算过程);
的所有可能值(不需要写计算过程);
(2)若![]() 是公差为1的等差数列,求
是公差为1的等差数列,求![]() 的通项公式;
的通项公式;
(3)证明:存在满足条件的数列![]() ,使得在该数列中,有无穷多项为2019.
,使得在该数列中,有无穷多项为2019.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一列函数![]() ,设直线
,设直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 在
在![]() 轴和直线
轴和直线![]() 上的射影分别为
上的射影分别为![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的最小值,并指出此时
的最小值,并指出此时![]() 的取值;
的取值;
(2)在![]() 中任取一个函数,求该函数在
中任取一个函数,求该函数在![]() 上是增函数或在
上是增函数或在![]() 上是减函数的概率;
上是减函数的概率;
(3)是否存在正整数![]() ,使得
,使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某沿海地区计划铺设一条电缆联通A,B两地,A地位于东西方向的直线MN上的陆地处,B地位于海上一个灯塔处,在A地用测角器测得![]() ,在A地正西方向4km的点C处,用测角器测得
,在A地正西方向4km的点C处,用测角器测得![]() .拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设
.拟定铺设方案如下:在岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km,设![]() ,
,![]() ,铺设电缆的总费用为
,铺设电缆的总费用为![]() 万元.
万元.

(1)求函数![]() 的解析式;
的解析式;
(2)试问点P选在何处时,铺设的总费用最少,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com