
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 也是抛物线
也是抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 与
与![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)平面上的点![]() 满足
满足![]() ,直线
,直线![]() ,且与
,且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
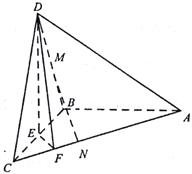
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
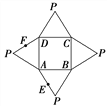
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 的直线与圆
的直线与圆![]() 相切,且与直线
相切,且与直线![]() 垂直,则
垂直,则![]() ( )
( )
A. 2 B. 1 C. ![]() D.
D. ![]()
【答案】A
【解析】因为点P(2,2)满足圆![]() 的方程,所以P在圆上,
的方程,所以P在圆上,
又过点P(2,2)的直线与圆![]() 相切,且与直线axy+1=0垂直,
相切,且与直线axy+1=0垂直,
所以切点与圆心连线与直线axy+1=0平行,
所以直线axy+1=0的斜率为: ![]() .
.
故选A.
点睛:对于直线和圆的位置关系的问题,可用“代数法”或“几何法”求解,直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,解题时不要单纯依靠代数计算,若选用几何法可使得解题过程既简单又不容易出错.
【题型】单选题
【结束】
23
【题目】设![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点.若点
的左、右焦点.若点![]() 在双曲线上,且
在双曲线上,且![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一个居民月用电量标准![]() ,用电量不超过
,用电量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以
的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
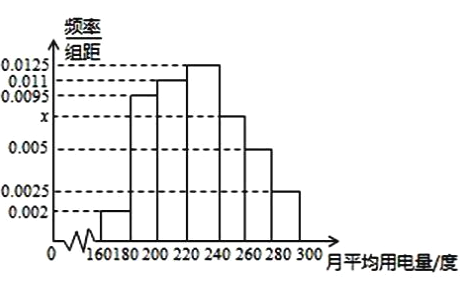
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)如果当地政府希望使![]() 左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准
左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准![]() 应该定为多少合理?
应该定为多少合理?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.
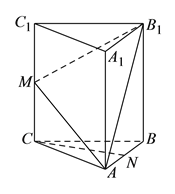
(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com