考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明BN⊥平面A1B1C1,只需证明BN⊥A1B1,BN⊥MN,
(Ⅱ)建立坐标系,求出平面ABA1的一个法向量、平面MAB的法向量,利用向量的夹角公式,即可求二面角A1-AB-M的余弦值.
解答:
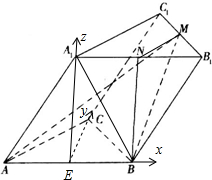
(Ⅰ)证明:连接MN,A
1B,
∵侧面是ABB
1A
1菱形,且∠A
1AB=60°,
∴△A
1BB
1为正三角形.
∵N是A
1B
1的中点,
∴BN⊥A
1B
1,
∵AA
1=AB=BM=2,
∴BN=
,MN=1,
∴BN
2+MN
2=BM
2,
∴BN⊥MN,
∵A
1B
1∩MN=N,
∴BN⊥平面A
1B
1C
1;
(Ⅱ)解:取AB的中点E,连接A
1E,则A
1E∥BN,由(Ⅰ)知A
1E⊥平面ABC,
以E为坐标原点,建立如图所示的坐标系,则E(0,0,0),A(-1,0,0),B(1,0,0),C(0,
,0),A(0,0,
),B
1(2,0,
),
设M(x,y,z),由
=得x=
,y=
,z=
,
∴M(
,
,
),
∴
=(
,
,
),
=(
,
,
),
平面ABA
1的一个法向量为
=(0,1,0).
设平面MAB的法向量
=(x,y,z),则
,
∴
=(0,-2,1),
∴cos<
,
>=
=
,
∴二面角A
1-AB-M的余弦值为
.
点评:本题考查线面垂直,考查面面角,考查向量法的运用,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

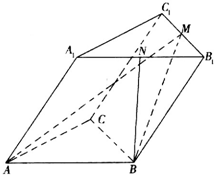 如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°.
如图,已知斜三棱柱ABC-A1B1C1的底面是正三角形,点M、N分别是B1C1和A1B1的中点,AA1=AB=BM=2,∠A1AB=60°. (Ⅰ)证明:连接MN,A1B,
(Ⅰ)证明:连接MN,A1B,

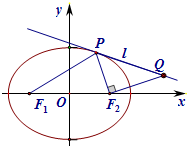 在平面直角坐标系xoy中,已知F1,F2分别是椭圆G:
在平面直角坐标系xoy中,已知F1,F2分别是椭圆G: