练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将圆上每个点的横坐标变为原来的4倍，纵坐标变为原来的3倍，得曲线，以坐标原点为极点， 轴的非负轴分别交于半轴为极轴建立极坐标系，直线的极坐标方程为： ，且直线在直角坐标系中与轴分别交于两点.

    （1）写出曲线的参数方程，直线的普通方程；

    （2）问在曲线上是否存在点，使得的面积，若存在，求出点的坐标，若不存在，请说明理由.

    【答案】（1）曲线的参数方程为，直线的普通方程为。（2）点的坐标为。

    【解析】试题分析：（1）根据伸缩变换可以得到曲线为椭圆，故其参数方程为，对于极坐标方程，展开后利用可转化为普通方程.（2）利用椭圆的参数方程设出动点的坐标，根据三角形的面积为求出其到直线的距离为，也即是，从而求出，也就得到的坐标.

    解析：（1）曲线 ，故曲线 的参数方程为 (为参数)

    直线 的普通方程为： .

    （2）设曲线 上点 ，点到直线的距离为，则，又 ，故 ，当 时取等号，即 ，此时 ，故在曲线上存在点，使得的面积，点的坐标为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校为了鼓励学生热心公益，服务社会，成立了“慈善义工社”.2017年12月，该校“慈善义工社”为学生提供了4次参加公益活动的机会，学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况，该校随机抽取100名学生进行调查，数据统计如下表，其中“√”表示参加，“×”表示未参加.

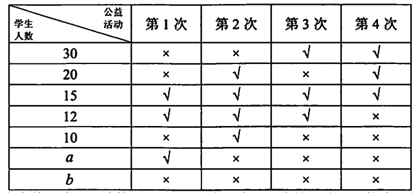
    根据表中数据估计，该校4000名学生中约有120名这4次活动均未参加.

    （Ⅰ）求的值；

    （Ⅱ）从该校4000名学生中任取一人，试估计其2017年12月恰参加了2次学校组织的公益活动的概率；

    （Ⅲ）已知学生每次参加公益活动可获得10个公益积分，任取该校一名学生，记该生2017年12月获得的公益积分为，求随机变量的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在[1，＋∞)上的函数f(x)满足：①f(2x)＝2f(x)；②当2≤x≤4时，f(x)＝1－|x－3|.则函数g(x)＝f(x)－2在区间[1,28]上的零点个数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

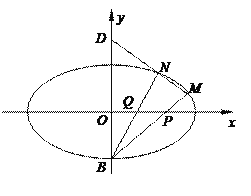
    【题目】如图，在平面直角坐标系中，椭圆的下顶点为，点是椭圆上异于点的动点，直线分别与轴交于点，且点是线段的中点．当点运动到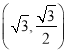点处时，点的坐标为．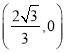

    （1）求椭圆的标准方程；

    （2）设直线交轴于点，当点均在轴右侧，且时，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】共享单车因绿色、环保、健康的出行方式，在国内得到迅速推广.最近，某机构在某地区随机采访了10名男士和10名女士，结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”，其他人表示“较少或不选择骑共享单车出行”.

    （1）从这些男士和女士中各抽取一人，求至少有一人“经常骑共享单车出行”的概率；

    （2）从这些男士中抽取一人，女士中抽取两人，记这三人中“经常骑共享单车出行”的人数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示为一正方体的平面展开图，在这个正方体中，有下列四个命题：

    ①AF⊥GC；

    ②BD与GC成异面直线且夹角为60；

    ③BD∥MN；

    ④BG与平面ABCD所成的角为45.

    其中正确的个数是( )

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正四棱锥的各条棱长都相等，且点分别是的中点.

    （1）求证: ；

    （2）在上是否存在点，使平面平面，若存在，求出的值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1， 在直角梯形中， ， ， ， 为线段的中点. 将沿折起，使平面 平面，得到几何体，如图2所示.

    （1）求证: 平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在“新零售”模式的背景下，某大型零售公司为推广线下分店，计划在市的区开设分店．为了确定在该区开设分店的个数，该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格．记表示在各区开设分店的个数， 表示这个分店的年收入之和．

    （个）

    2

    3

    4

    5

    6

    （百万元）

    2.5

    3

    4

    4.5

    6

    （Ⅰ）该公司已经过初步判断，可用线性回归模型拟合与的关系，求关于的线性回归方程；

    （Ⅱ）假设该公司在区获得的总年利润（单位：百万元）与之间的关系为，请结合（Ⅰ）中的线性回归方程，估算该公司应在区开设多少个分店，才能使区平均每个分店的年利润最大？

    参考公式：

    ， ， ．

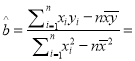
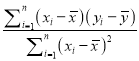    查看答案和解析>>

    同步练习册答案