
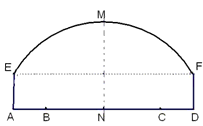
 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为 m,行车道总宽度BC为
m,行车道总宽度BC为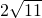 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.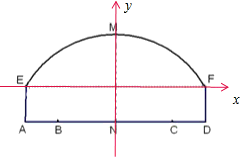 解:(1)以EF所在直线为x轴,以MN所在直线为y轴,
解:(1)以EF所在直线为x轴,以MN所在直线为y轴, ,0),F(3
,0),F(3 ,0),M(0,3),
,0),M(0,3), ,
, 代入圆的方程,
代入圆的方程,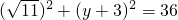 ,
, 代入圆的方程,求出y,然后求出限高.
代入圆的方程,求出y,然后求出限高.

科目:高中数学 来源: 题型:
 如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为6
如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为6| 3 |
| 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
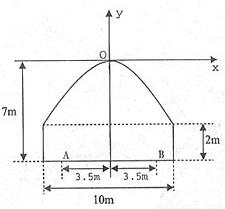
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省泉州市惠安县惠南中学高二(上)期末数学试卷(选修2-1)(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建师大附中高一(上)期末数学试卷(解析版) 题型:解答题
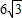 m,行车道总宽度BC为
m,行车道总宽度BC为 m,侧墙EA、FD高为2m,弧顶高MN为5m.
m,侧墙EA、FD高为2m,弧顶高MN为5m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com