
【题目】已知椭圆![]() 的左右顶点为A,B,点P,Q为椭圆上异于A,B的两点,直线AP、BP、BQ的斜率分别记为
的左右顶点为A,B,点P,Q为椭圆上异于A,B的两点,直线AP、BP、BQ的斜率分别记为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求证:
,求证:![]() ,并判断直线PQ是否过定点,若是,求出该定点;若不是,请说明理由.
,并判断直线PQ是否过定点,若是,求出该定点;若不是,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提倡节能减排,同时减轻居民负担,广州市积极推进“一户一表”工程。非一户一表用户电费采用“合表电价”收费标准:0.65元/度。“一户一表”用户电费采用阶梯电价收取,其11月到次年4月起执行非夏季标准如下:
第一档 | 第二档 | 第三档 | |
每户每月用电量(单位:度) |
|
|
|
电价(单位:元/度) | 0.61 | 0.66 | 0.91 |
例如:某用户11月用电410度,采用合表电价收费标准,应交电费![]() 元,若采用阶梯电价收费标准,应交电费
元,若采用阶梯电价收费标准,应交电费![]() 元.
元.
为调查阶梯电价是否能取到“减轻居民负担”的效果,随机调查了该市100户的11月用电量,工作人员已经将90户的月用电量填在下面的频率分布表中,最后10户的月用电量(单位:度)为:88、268、370、140、440、420、520、320、230、380.
组别 | 月用电量 | 频数统计 | 频数 | 频率 |
① |
|
| ||
② |
|
| ||
③ |
|
| ||
④ |
|
| ||
⑤ |
|
| ||
⑥ |
|
| ||
合计 |
(1)完成频率分布表,并绘制频率分布直方图;

(2)根据已有信息,试估计全市住户11月的平均用电量(同一组数据用该区间的中点值作代表);
(3)设某用户11月用电量为![]() 度(
度(![]() ),按照合表电价收费标准应交
),按照合表电价收费标准应交![]() 元,按照阶梯电价收费标准应交
元,按照阶梯电价收费标准应交![]() 元,请用
元,请用![]() 表示
表示![]() 和
和![]() ,并求当
,并求当![]() 时,
时,![]() 的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于75%的用户带来实惠?
的最大值,同时根据频率分布直方图估计“阶梯电价”能否给不低于75%的用户带来实惠?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.

(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴![]() 万元,购买外地企业生产的每台补贴
万元,购买外地企业生产的每台补贴![]() 万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过
万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过![]() 万元.则购买外地产的新能源汽车每台最多补贴多少万元?
万元.则购买外地产的新能源汽车每台最多补贴多少万元?
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.
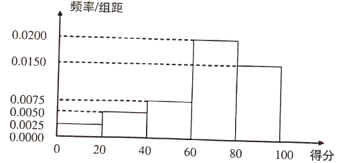
(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)把满意度得分少于![]() 分的用户很不满意用户,在很不满意的用户中有
分的用户很不满意用户,在很不满意的用户中有![]() 户购买使用本市企业生产的新能源汽车,其他是购买外地产的.现在从样本中很不满意的用户中随机抽取
户购买使用本市企业生产的新能源汽车,其他是购买外地产的.现在从样本中很不满意的用户中随机抽取![]() 户进行了解很不满意的具体原因,求这
户进行了解很不满意的具体原因,求这![]() 户恰好是一户购买本市企业产的,另一户是购买外地企业产的概率.
户恰好是一户购买本市企业产的,另一户是购买外地企业产的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x)=f(2-x),且f(1)=6,f(3)=2.
(1)求f(x)的解析式
(2)是否存在实数m,使得在[-1,3]上f(x)的图象恒在直线y=2mx+1的上方?若存在,求m的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com