
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,满足
上,满足![]() ,
,![]() 交
交![]() 于点
于点![]() .将
.将![]() 沿
沿![]() 折到
折到![]() 的位置,
的位置, ![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
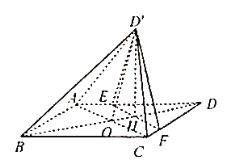
科目:高中数学 来源: 题型:
【题目】某工厂共有员工5000人,现从中随机抽取100位员工,对他们每月完成合格产品的件数进行统计,统计表格如下:

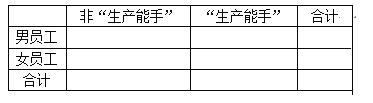
(1)工厂规定:每月完成合格产品的件数超过3200件的员工,会被评为“生产能手”称号.由以上统计数据填写下面的![]() 列联表,并判断是否有95%的把握认为“生产能手”称号与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”称号与性别有关?
(2)为提高员工劳动的积极性,该工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的(包括2600件),计件单价为1元;超出(0,200]件的部分,累进计件单价为1.2元;超出(200,400]件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段的频率视为相应的概率,在该厂男员工中随机选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)超过3100元的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
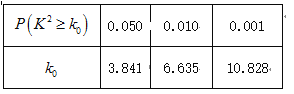
附:![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的命题是( )
A.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3;
和0.3;
B.事件![]() 为必然事件,则事件
为必然事件,则事件![]() 、
、![]() 是互为对立事件;
是互为对立事件;
C.设随机变量![]() ,若
,若![]() ,则
,则![]() ;
;
D.甲、乙、丙、丁4个人到4个景点旅游,每人只去一个景点,设事件![]() “4个人去的景点各不相同”,事件
“4个人去的景点各不相同”,事件![]() “甲独自去一个景点”,则
“甲独自去一个景点”,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽在《周髀算经》中注释了其理论证明,其基本思想是图形经过割补后面积不变.即通过如图所示的“弦图”,将匀股定理表述为:“勾股各自乘,并之,为弦实,开方除之,即弦”(其中![]() 分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即
分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即![]() ,化简得
,化简得![]() .现已知
.现已知![]() ,
,![]() ,向外围大正方形
,向外围大正方形![]() 区域内随机地投掷一枚飞镖,飞镖落在中间小正方形
区域内随机地投掷一枚飞镖,飞镖落在中间小正方形![]() 内的概率是( )
内的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知动直线
中,已知动直线![]() 的参数方程:
的参数方程:![]() ,(
,(![]() 为参数,
为参数,![]() ) ,以坐标原点为极点,
) ,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 恰好有2个公共点时,求直线
恰好有2个公共点时,求直线![]() 的一般方程.
的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的图像经过点
)的图像经过点![]() ,且关于直线
,且关于直线![]() 对称,则下列结论正确的是( )
对称,则下列结论正确的是( )
A. ![]() 在
在![]() 上是减函数
上是减函数
B. 函数的最小正周期为![]()
C. ![]() 的解集是
的解集是![]() ,
,![]()
D. ![]() 的一个对称中心是
的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com