
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() . 已知过点
. 已知过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.

(1)求椭圆![]() 的方程;
的方程;
(2)试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值.若存在,求出点
为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)先根据已知得到三个方程解方程组即得椭圆C的方程. (2) 设N(n,0),先讨论l斜率不存在的情况得到n=4,再证明当N为(4,0)时,对斜率为k的直线l:y=k(x-![]() ),恒有
),恒有![]() =12.
=12.
详解:(1)离心率e=![]() ,所以c=
,所以c=![]() a,b=
a,b=![]() =
=![]() a,
a,
所以椭圆C的方程为![]() .
.
因为椭圆C经过点![]() ,所以
,所以![]() \,
\,
所以b2=1,所以椭圆C的方程为![]() .
.
(2)设N(n,0),
当l斜率不存在时,A(![]() ,y),B(
,y),B(![]() ,-y),则y2=1-
,-y),则y2=1-![]() =
=![]() ,
,
则![]() =(
=(![]() -n)2-y2=(
-n)2-y2=(![]() -n)2-
-n)2-![]() =n2-
=n2-![]() n-
n-![]() ,
,
当l经过左span>右顶点时,![]() =(-2-n)(2-n)=n2-4.
=(-2-n)(2-n)=n2-4.
令n2-![]() n-
n-![]() =n2-4,得n=4.
=n2-4,得n=4.
下面证明当N为(4,0)时,对斜率为k的直线l:y=k(x-![]() ),恒有
),恒有![]() =12.
=12.
设A(x1,y1),B(x2,y2),
由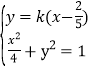 消去y,得(4k2+1)x2-
消去y,得(4k2+1)x2-![]() k2x+
k2x+![]() k2-4=0,
k2-4=0,
所以x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
所以![]() =(x1-4)(x2-4)+y1y2
=(x1-4)(x2-4)+y1y2
=(x1-4)(x2-4)+k2(x1-![]() )(x2-
)(x2-![]() )
)
=(k2+1)x1x2-(4+![]() k2)(x1+x2)+16+
k2)(x1+x2)+16+![]() k2
k2
=(k2+1) ![]() -(4+
-(4+![]() k2)
k2) ![]() +16+
+16+![]() k2
k2
=![]() +16=12.
+16=12.
所以在x轴上存在定点N![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 过原点,倾斜角为
过原点,倾斜角为![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,半径为2,以坐标原点为极点,
,半径为2,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)分别写出直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() 为极轴与圆
为极轴与圆![]() 的交点(异于极点),点
的交点(异于极点),点![]() 为直线与圆
为直线与圆![]() 在第二象限的交点,求
在第二象限的交点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”其意思为:“今有白米一百八十石,甲、乙、丙三人来分,他们分得的白米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”请问:乙应该分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量![]() =(a,
=(a,![]() b)与
b)与![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a=![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com