
【题目】已知函数![]()
![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 与
与![]() 图象在
图象在![]() 上有两个不同的交点,求实数
上有两个不同的交点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)y=2x-1. (Ⅱ)[![]() ].
].
【解析】【试题分析】(I)当![]() 时,求出
时,求出![]() 和
和![]() 的值,利用点斜式求得切线方程.(II)令
的值,利用点斜式求得切线方程.(II)令![]() ,化简得
,化简得![]() ,构造函数
,构造函数![]() ,利用导数求得
,利用导数求得![]() 在区间
在区间![]() 上的极大值为
上的极大值为![]() ,通过计算
,通过计算![]() 和
和![]() 可知
可知![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,由此可用最大值大于零,最小值不大于零列不等式组,求得
,由此可用最大值大于零,最小值不大于零列不等式组,求得![]() 的取值范围.
的取值范围.
【试题解析】
(Ⅰ)解 当![]() 时,f(x)=2lnx-x2+2x,f′(x)=
时,f(x)=2lnx-x2+2x,f′(x)=![]() -2x+2,
-2x+2,
切点坐标为(1,1),切线的斜率k=f′(1)=2,
则切线方程为y-1=2(x-1),即y=2x-1.
(Ⅱ)解:由题意可得:2lnx-x2+m=0,令h(x)=2lnx-x2+m,
则h′(x)=![]() -2x=
-2x=![]() ,
,
∵x∈![]() ,故h′(x)=0时,x=1.
,故h′(x)=0时,x=1.
当![]() <x<1时,h′(x)>0;当1<x<e时,h′(x)<0.
<x<1时,h′(x)>0;当1<x<e时,h′(x)<0.
故h(x)在x=1处取得极大值h(1)=m-1.
又![]() =m-2-
=m-2-![]() ,h(e)=m+2-e2,h(e)-
,h(e)=m+2-e2,h(e)-![]() =4-e2+
=4-e2+![]() <0,
<0,
则h(e)<![]() ,
,
∴h(x)在[![]() ]上的最小值为h(e).
]上的最小值为h(e).
h(x)在[![]() ]上有两个零点的条件是
]上有两个零点的条件是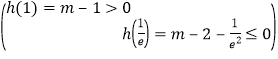 ,
,
解得1<m≤2+![]()
∴实数m的取值范围是[![]() ].
].


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )

A. 10000立方尺 B. 11000立方尺
C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国的钨矿资源储量丰富,在全球已经探明的钨矿产资源储量中占比近![]() ,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当
,居全球首位。中国又属赣州钨矿资源最为丰富,其素有“世界钨都”之称。某科研单位在研发的钨合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值与这种新合金材料的含量x(单位:克)的关系为:当![]() 时,
时, ![]() 是
是![]() 的二次函数;当
的二次函数;当![]() 时,
时, ![]() .测得部分数据如表.
.测得部分数据如表.
x(单位:克) | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
(1)求y关于x的函数关系式y=![]()
(2)求函数![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 是直线
是直线![]() 上的点,且
上的点,且![]() ,当
,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com