
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 左、右焦点,点
左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的两个动点,如果直线
的两个动点,如果直线![]() 与直线
与直线![]() 的倾斜角互补,证明:直线
的倾斜角互补,证明:直线![]() 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据点![]() 在椭圆上,以及
在椭圆上,以及![]() 轴,可以求出
轴,可以求出![]() 的值,再根据
的值,再根据![]() 的周长为
的周长为![]() 以及椭圆的定义可以求出
以及椭圆的定义可以求出![]() ,进而可以得到椭圆的标准方程;(2)根据题目条件可知直线
,进而可以得到椭圆的标准方程;(2)根据题目条件可知直线![]() 与直线
与直线![]() 的斜率应是互为相反数,据此可以得到点
的斜率应是互为相反数,据此可以得到点![]() 坐标,进而可以求出直线
坐标,进而可以求出直线![]() 的斜率为定值,即证明了直线
的斜率为定值,即证明了直线![]() 的斜率为定值.
的斜率为定值.
试题解析:(1)由题意,![]() ,...............1分
,...............1分
![]() …………… 2分
…………… 2分
∴![]() ............3分
............3分
∴ 椭圆方程为![]() ,..........................4分
,..........................4分
(2)由(1)知![]() ,设直线
,设直线![]() 方程:得
方程:得![]() ,代入
,代入![]() 得
得
 .....................6分
.....................6分
设![]() ,因为点
,因为点![]() 在椭圆上,所以
在椭圆上,所以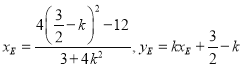 ,
,
又直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,在上式中以
的斜率互为相反数,在上式中以![]() 代
代![]() ,可得
,可得
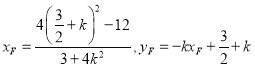 ...................9分
...................9分
所以直线![]() 的斜率
的斜率![]() ,
,
即直线![]() 的斜率为定值,其值为
的斜率为定值,其值为![]() .......................10分
.......................10分


科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:cm)满足关系
(单位:cm)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元,设
,若不建隔热层,每年能源消耗费用为8万元,设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
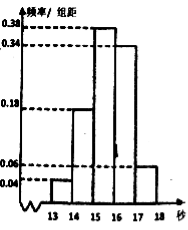
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=![]() ,anbn+1+bn+1=nbn.
,anbn+1+bn+1=nbn.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,设
,设![]() 为
为![]() 的前
的前![]() 项和.
项和.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)求![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]()
![]() ,使
,使![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
,![]() ,
,![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com